The CPI is useful both as an indicator of how much prices change in the aggregate, and also as an indicator of relative price changes. Column 4 of Table 2.1 provides the Vancouver CPI with the same base year as the North Vancouver house price index. Note how the two indexes move very differently over time. The price of housing has increased considerably relative to the overall level of prices in the local economy, as measured by the CPI: Housing has experienced a relative price increase, or a real price index. This real increase is to be distinguished from the nominal price index, which is measured without reference to overall prices. The real price index for housing (or any other specific product) is obtained by dividing its specific price index by the CPI.
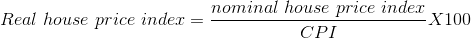
 Real price index: a nominal price index divided by
the consumer price index, scaled by 100.
Real price index: a nominal price index divided by
the consumer price index, scaled by 100.
 Nominal price index: the current dollar price of a
good or service.
Nominal price index: the current dollar price of a
good or service.
The resulting index is given in column 5 of Table 2.1. This index has a simple interpretation: It tells us by how much the price of Vancouver houses has changed relative to the general level of prices for goods and services. For example, between 1999 and 2004 the number 119.55 in column 5 for the year 2004 indicates that housing increased in price by 19.55 percent relative to prices ingeneral.
Here is a further simple example. Table 2.3 reports recent annual data on indexes of nominal earnings, measured in current dollars, both average weekly and hourly rates, over the 2003-2011 time period. The table also reports the consumer price index for the same time period. To simplify the illustration all indexes have been re-based to 2003=100 by dividing the reported value of the index in each year by its value in 2003 and multiplying by 100.
The table shows the difference between changes in nominal and real earnings. Real earnings are measured in constant dollars adjusted for changes in the general price level. The adjustment is made by dividing the indexes of nominal earnings in each year by the consumer price index in that year and multiplying by 100.
 Nominal earnings: earnings measured in current
dollars.
Nominal earnings: earnings measured in current
dollars.
 Real earnings: earnings measure in constant
dollars to adjust for changes in the general price level.
Real earnings: earnings measure in constant
dollars to adjust for changes in the general price level.
As measured by the nominal weekly and hourly indexes, nominal earnings increased by 26 to 27 percent over the eight year period 2003-2011. However, the general price level as measured by the consumer price index (CPI) increased by close to 17 percent over the same period. As a result, real earnings, measured in terms of the purchasing power of nominal earnings increased by only about 9 percent, notable less than in 26 percent increase in nominal earnings.
| Nominal earnings | Real earnings | ||||
| Year | Average weekly earnings | Average hourly earnings | CPI | Average weekly earnings | Average hourly earnings |
| 2003 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| 2004 | 102.7 | 102.7 | 101.8 | 100.8 | 100.9 |
| 2005 | 106.7 | 106.2 | 106.2 | 102.4 | 101.9 |
| 2006 | 1009.4 | 108.8 | 104.2 | 103.0 | 102.5 |
| 2007 | 114.1 | 113.8 | 108.5 | 105.2 | 104.9 |
| 2008 | 117.4 | 117.7 | 111.0 | 105.7 | 106.1 |
| 2009 | 119.2 | 121.3 | 111.3 | 107.1 | 109.0 |
| 2010 | 123.5 | 125.0 | 111.3 | 109.0 | 110.3 |
| 2011 | 126.6 | 127.5 | 116.6 | 108.6 | 109.4 |
Source: Statistics Canada, CANSIM Series V1558664, V1606080 and V41690914 and author’s calculations
These observations illustrate two important points. First the distinction between real and nominal values is very important. If the general price level is changing, changes in real values will differ from changes in nominal values. Real values change by either less or more than changes in nominal values. Second, in addition to tracking change over time, index numbers used in combination simplify the adjustment from nominal to real values, as shown in both Table 2.1 and Table 2.3.
However, a word of caution is necessary. Index numbers can be used to track both nominal and real values over time but they do not automatically adjust for change in the quality of products and services or the changing patterns of output and use in the cases of composite indexes. Index number bases and weights need constant adjustment to deal with these issues.
- 瀏覽次數:2341






