The increase in inequality of earnings in the market place in Canada has been reflected in many other developed economies – to a greater degree in the US and to a lesser extent in some European economies. Economists have devoted much energy to studying why, and as a result there are several accepted reasons.
Younger workers and those with lower skill levels have fared poorly in the last three decades. It has been proposed that globalization and out-sourcing have been responsible for this. In effect the workers in the lower tail of the distribution are increasingly competing with workers from low wage less-developed economies. While this is a plausible causation, the critics of the perspective point out that wages at the bottom have fallen not only for those workers who compete with overseas workers in manufacturing, but also in the domestic services sector right across the economy.
Obviously the workers at McDonalds have not the same competition from low-wage economies as workers who assemble toys.
A competing perspective is that it is technological change that has enabled some workers to do better than others. In explaining why high wage workers in many economies have seen their wages increase, whereas low-wage workers have seen a relative decline, the technological change hypothesis proposes that the form of recent technological change is critical: change has been such as to require other complementary skills and education in order to benefit from it. For example, the introduction of computer-aided design technology is a benefit to workers who are already skilled and earning a high wage: existing high skills and technological change are complementary. Such technological change is therefore different from the type underlying the production line. Automation in the early twentieth century in Henry Ford’s plants improved the wages of lower skilled workers. But in the modern economy it is the highly skilled rather than the low skilled that benefit most from innovation.
A third perspective is that key institutional changes manifested themselves in the eighties and nineties, and these had independent impacts on the distribution. In particular, changes in the extent of unionization and changes in the minimum wage have significant impacts on earnings in the middle and bottom of the distribution: If unionization declines or the minimum wage fails to keep up with inflation, these workers will suffer. An alternative ‘institutional’ player is the government: in Canada the federal government became less supportive or generous with its array of programs that form Canada’s social safety net in the nineteen nineties. This tightening goes some way to explaining the increasing inequality in the post-tax income distribution in Figure 13.3 at this time.
We conclude this overview of distributional issues by pointing out that we have not touched upon the distribution of wealth. Wealth too represents purchasing power, and it is wealth rather than income flows that primarily distinguishes Warren Buffet, Mark Zuckerberg and Bill Gates from the rest of us mortals.
KEY TERMS
Human capital is the stock of expertise accumulated by a worker that determines future productivity and earnings.Age-earnings profiles define the pattern of earnings over time for individuals with different characteristics.
Education premium: the difference in earnings between the more and less highly educated.
On-the-job training improves human capital through work experience.
Firm-specific skills raise a worker’s productivity in a particular firm.
General skills enhance productivity in many jobs or firms.
Signalling is the decision to undertake an action in order to reveal information.
Screening is the process of obtaining information by observing differences in behaviour.
Discrimination implies an earnings differential that is attributable to a trait other than human capital.
Lorenz curve describes the cumulative percentage of the income distribution going to different quantiles of the population.
Gini index: a measure of how far the Lorenz curve lies from the line of equality. Its maximum value is one; its minimum value is zero.
EXERCISES
- In the short run one half of the labour force has high skills and one half low skills (in terms of Figure 13.2 this means that the short-run supply curve is vertical at 0.5). The
relative demand for the high-skill workers is given byW = 100 X 0.4 X (1 - f ), where W is the wage premium and f is the fraction that is skilled. The premium is measured in percent.
- Illustrate the supply and demand curves graphically, and compute the skill premium going to the high-skill workers in the short run by solving the two equations.
- If demand increases to W = 100 X 0.6 X (1 - f ) what is the new premium? Illustrate your answer graphically.
- Consider the foregoing problem in a long run context, when the fraction of the labour force that is high-skilled is more elastic with respect to the premium. Let this long-run
relative supply function beW = 100 X 0.4 X f .
- Verify that this long run function goes through the same equilibrium as in the preceding question.
- Illustrate the long run and short run on the same diagram.
- What is the numerical value of the premium in the long run after the increase in demand? Illustrate graphically.
- Consider a world in which there are two types of workers – high skill and low skill. Low skill workers are willing to work for $10 per hour and high-skill workers for $18 per
hour. Any firm that demands both types of worker has a demand curve (value of the
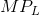 ) for each type. Suppose that the demand for high-skill workers lies everywhere above the demand for low-skill workers.
Illustrate on a diagram the supply and demand functions for each type of labour, and the equilibrium for each type of worker.
) for each type. Suppose that the demand for high-skill workers lies everywhere above the demand for low-skill workers.
Illustrate on a diagram the supply and demand functions for each type of labour, and the equilibrium for each type of worker.
- Georgina is contemplating entering the job market after graduating from high school. Her future lifespan is divided into three periods. If she goes to university for the
first, and earns an income for the following two periods her lifetime balance sheet will be: (i) -$20,000; (ii) $40,000; (iii) $50,000. The negative value implies that she will incur costs in
educating herself in the first period. In contrast, if she decides to work for all three periods she will earn $20,000 in each period. The answer here involves discounting, and you should
assume that the first period is today, the second period amount must be discounted back one period, and the final amount discounted back two periods.
- If the interest rate is 10% should she go to university or enter the job market immediately?
- If the interest rate is 2% what should she do?
- Can you find some value for the interest rate that will change her decision?
- Laurence has decided that he will definitely go to university rather than go into the workforce directly after high school. He is trying to decide between Law and Economics.
LikeGeorgina, his life can be divided into three parts. He will incur education costs in the first period and earn in the remaining two periods. His income profile is given in the table
below.(Discounting need not be applied to the first number, but the following numbers must be discounted back one period and two periods respectively.)
- If the interest rate is 2%, which profession should he choose?
- If the interest rate is 30% which profession should he choose?
- Imagine that you have the following data on the income distribution for two economies. The first set of quintile shares is as in Table 13.2, and the second set is: 3.0, 9.0, 17.0, 29.0, and
42.0.
- On graph paper, or in a spreadsheet program, plot the Lorenz curves corresponding tothe two sets of quintile shares.
- Can you say, from a visual analysis, which distribution is more equal?
- The distribution of income in the economy is given in the table below. The first numerical column represents the dollars earned by each quintile. Since the numbers add to 100
you can equally think of the dollar values as shares of the total pie. In this economy the government changes the distribution by levying taxes and distributing benefits.
- Plot the Lorenz curve for gross income to scale.
- Plot the Lorenz curve for income after taxes have been levied. Note that the total income will now be less than 100 and so you will have to compute the quintile shares using a new total.
- Finally, add in the benefits so that the total post-tax and post-benefit incomes sum to$100m again, and plot the Lorenz curve based on this final set of numbers.
- Here is a question on earnings profiles. Consider two individuals, each facing a 45 year horizon at the age of 20. Ivan decides to work immediately and his earnings path takes
the following form: earnings = 20,000+1,000t -
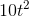 , where the
t is time, and it takes onvalues from 1 to 25, reflecting the working lifespan.
, where the
t is time, and it takes onvalues from 1 to 25, reflecting the working lifespan.
- In a spreadsheet enter values 1. . . 25 in the first column and then compute the value of earnings in each of the 45 years in the second column using the earnings equation.
- John decides to study some more and only earns a part-time salary in his first few years. He hopes that the additional earnings in future years will compensate for that.
His function is given by 10,000+2,000t -
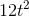 . Compute his
earnings for his lifespan.
. Compute his
earnings for his lifespan.
- Plot the two earnings functions you have computed. During what year does John pass Ivan?
- 瀏覽次數:2612






