The duopoly model that we frequently use in economics to analyze competition between a small number of competitors is fashioned after the ideas of French economist Augustin Cournot. Consequently it has come to be known as the Cournot duopoly model. While the maximizing behavior that is incorporated in this model can apply to a situation with several firms rather than two, we will develop the model with two firms. This model that we now explore differs somewhat from what we developed in the preceding section, where each firm has simply a choice between a high or low output. In addition that game had a dominant strategy for each participant, an infrequent event in most markets.
The critical element of the Cournot approach is that the firms each determine their optimal strategy – one that maximizes profit – by reacting optimally to their opponent’s strategy, which in this case is also their choice of output.
 Cournot behaviour involves each firm reacting
optimally in their choice of output to their competitors’ output decisions.
Cournot behaviour involves each firm reacting
optimally in their choice of output to their competitors’ output decisions.
A central element here is the reaction function of each firm, which defines the optimal output choice conditional upon their opponent’s choice.
 Reaction functions define the optimal choice of
output conditional upon a rival’s output choice.
Reaction functions define the optimal choice of
output conditional upon a rival’s output choice.
We can develop an optimal strategy with the help of Figure 11.3. D is the market demand, and two firms supply this market. If B supplies a zero output, then A would face the whole demand, and would maximize profit
where MC = MR. Let this output be defined by 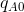 . We transfer this
output combination to Figure
11.4, where the output of each firm is on one of the axes—A on the vertical axis and B on the horizontal. This particular combination of zero output for B and
. We transfer this
output combination to Figure
11.4, where the output of each firm is on one of the axes—A on the vertical axis and B on the horizontal. This particular combination of zero output for B and 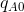 for A is represented on the vertical axis as the point
for A is represented on the vertical axis as the point 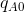 .
.
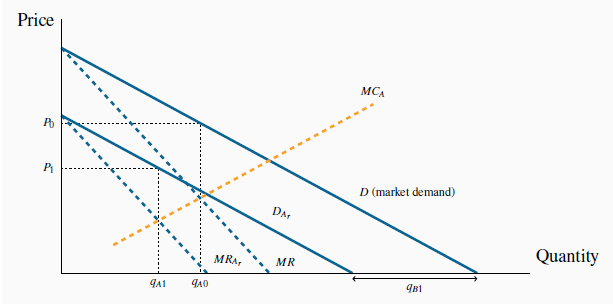
When one firm, B, chooses a specific output, e.g. 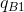 , then A’s
residual demand
, then A’s
residual demand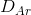 is the difference between the market demand and
is the difference between the market demand and
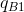 . A’s profit is maximized at
. A’s profit is maximized at 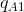 – where MC =
– where MC = 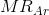 . This is an optimal reaction by A to B’s choice. For all possible choices by B, A can form a similar optimal response. The
combination of these responses forms A’s reaction function.
. This is an optimal reaction by A to B’s choice. For all possible choices by B, A can form a similar optimal response. The
combination of these responses forms A’s reaction function.
Instead, suppose that B produces a quantity 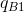 in Figure 11.3. This reduces the demand curve facing A correspondingly
from D to
in Figure 11.3. This reduces the demand curve facing A correspondingly
from D to 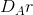 , which we call A’s residual demand. When subject to
such a choice by B, firm A maximizes profit by producing where
, which we call A’s residual demand. When subject to
such a choice by B, firm A maximizes profit by producing where 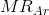 = MC, where
= MC, where 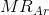 is the marginal revenue corresponding to the
residual demand
is the marginal revenue corresponding to the
residual demand 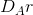 . The optimum for A is now
. The optimum for A is now 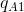 , and this pair of outputs is represented by the combination (
, and this pair of outputs is represented by the combination (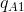 ,
, 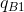 ) in Figure 11.4.
) in Figure 11.4.
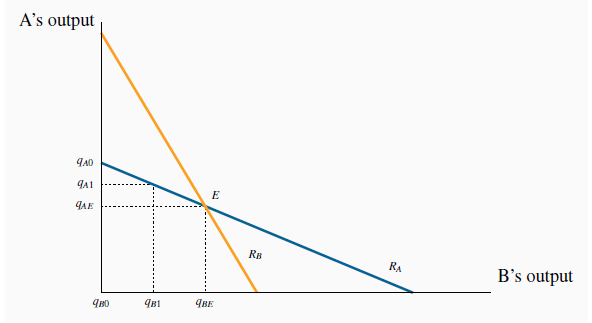
The reaction function for A (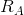 ) defines the optimal output response
for A to any output choice by B. The reaction function for B is defined similarly. The equilibrium occurs at the intersection of
) defines the optimal output response
for A to any output choice by B. The reaction function for B is defined similarly. The equilibrium occurs at the intersection of 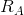 and
and 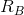 . Any other combination will induce one firm to change its output, and therefore could not be an equilibrium.
. Any other combination will induce one firm to change its output, and therefore could not be an equilibrium.
We can imagine A forming a similar optimal response for every possible output level that B could choose.
The reaction function illustrated for A in Figure 11.4 is thus the locus of all optimal response outputs on the part of A. The downward-sloping function makes sense: The more B produces, the smaller is the residual market for A, and therefore the less A will produce.
But A is just one of the players in the game. If B acts in the same optimizing fashion, B too can formulate a series of optimal reactions to A’s output choices. The combination of such choices
would yield a reaction function for B. This is plotted as 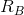 in
Figure 11.4.
in
Figure 11.4.
An equilibrium is defined by the intersection of the two reaction functions, in this case by the point E. At this output level each firm is making an optimal decision, conditional upon the choice of its opponent. Consequently, neither firm has an incentive to change its output; therefore it can be called the Nash equilibrium, as we defined earlier.
Any other combination of outputs on either reaction function would lead one of the players to change its output choice, and therefore could not constitute an equilibrium. To see this, suppose
that B produces an output greater than 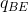 ; how will A react? A’s
reaction function indicates that it should choose a quantity to supply less than
; how will A react? A’s
reaction function indicates that it should choose a quantity to supply less than 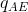 . If so, how will B respond in turn to that optimal choice? It responds with a quantity read from its reaction function, and this
will be less than the amount chosen at the previous stage. By tracing out such a sequence of reactions it is clear that the output of each firm will move to the equilibrium
. If so, how will B respond in turn to that optimal choice? It responds with a quantity read from its reaction function, and this
will be less than the amount chosen at the previous stage. By tracing out such a sequence of reactions it is clear that the output of each firm will move to the equilibrium 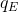 .
.
In this particular example, we assume each firm has the same cost structure. In addition they face the same market demand. Consequently their reaction functions are symmetric. To see how this model works numerically, consider the following example.
Let the marginal cost of each firm be constant at $6; thus MC = 6. Fixed costs are zero, and market demand will be given by
P = 24 - Q, that is P = 24-(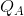 +
+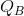 ).
).
The total amount traded, Q, is the sum of what each firm produces: Q = QA+QB. It follows that the residual demand facing A is
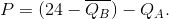
where the bar denotes a given amount on the part of B, and the MR curve is of similar form with twice the slope:
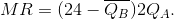
Profit is maximized where MC = MR, hence the choice of output for A is given as follows:
MC = MR implies 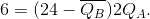
Rearranging yields A’s reaction function:
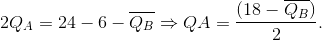
This is A’s reaction function. The reaction function for firm B can be obtained in exactly the same manner, and since the firms are assumed to have an identical cost structure in this example, B’s reaction function must be a mirror image of A’s:
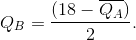
Solving the two reaction functions for their intersection point (E in Figure 11.4), yields the Nash equilibrium solution 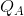 = 6 and
= 6 and 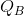 = 6.
= 6.
Finally, since the total output produced by the two suppliers is 12 units, the market demand curve indicates that this output must be sold at a price of $12 (P = 24 - 12). With a constant cost per unit of output, the profit of each firm is $36.
This example is particular in that it is symmetric – each firm has the same cost structure. But this need not be the case, and an interesting aspect of the Cournot model is that firms with different cost structures can survive side by side in the market. If we were to rework the above example with one of the firms having a higher marginal cost than the other we would find, not surprisingly, that the low-cost firm would obtain a greater market share than the high-cost producer. But the high cost producer here is not driven out of the market place. In contrast to perfect competition, where the presence of a large number of firms drives the price to a point where there are zero economic profits, the duopoly framework is a game played by just two competitors, and consequently each has market power.
Application Box: Cournot: fixed costs and brand
Why do we observe so many industries on the national, and even international, stages with only a handful of firms? For example, Intel produces more than half of the world’s computer chips, and AMD produces a significant part of the remainder. Why are there only two major commercial aircraft producers in world aviation-Boeing and Airbus? Why are there only a handful of major pharmaceutical manufacturers in North America?
The answer to these questions lies partly in the nature of modern product development. Product development (fixed) costs, coupled with a relatively small marginal cost of production, leads to markets where there is enough space for only a few players. The development cost for a new cell phone, or a new aircraft, or a new operating system may run into billions, while the cost of producing each unit may in fact be constant. The enormous development cost associated with many products explains not only why there may be a small number of firms in the domestic market for the product, but also why the number of firms in some sectors is small worldwide.
- 6201 reads






