It is not difficult to represent the supply and demand functions underlying Table 3.1 in their mathematical form:
Demand: P = 10 - Q
Supply: P = 1+(1/2)Q
In the previous chapter we stated that a straight line is represented completely by the intercept and slope. Let us first verify that these equations do, indeed, represent the data in Table 3.1. On the demand side, we see that a zero quantity is demanded at a price of $10, and this is therefore the intercept with the price (vertical) axis. To see this just set P = 10 in the demand equation. As for the slope, each unit change in quantity demanded (measured in thousands) is associated with a $1 change in price. For instance, when the price is increased by $2, the quantity demanded declines by 2 units. In reverse, if the price is lowered by $2, the quantity demanded increases by 2 units. Since the price is on the vertical axis, it follows that the slope is given by -$1/1 = - 1. It is negative because an increase in quantity demanded is associated with a decrease in price.
On the supply side, column 3 in Table 3.1 indicates that at a quantity of zero the price is $1. Therefore, $1 is the price intercept. As for the slope, each 2-unit change in quantity is associated with a change in price of $1. Consequently, the slope is given by $1/2=1/2. In this case the slope is positive, since both the price and quantity move in the same direction.
We have now obtained the two defining characteristics of the demand and supply curves, which enable us to write them as above. Next we must find where they intersect – the market equilibrium.
Since, at their intersection point, the price on the demand curve equals the price on the supply curve, and the quantity demanded equals the quantity supplied, this unique price-quantity
combination is obtained by equating the two curves:
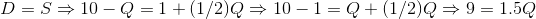
The  symbol is used in mathematics to denote
“implication”. For example, A
symbol is used in mathematics to denote
“implication”. For example, A  B translates to “If A, then
B.”
B translates to “If A, then
B.”
Therefore,
Q = 9/1.5 = 6
The equilibrium solution for Q is therefore 6 units. What about an equilibrium price? It is obtained by inserting the equilibrium Q value into either the supply or the demand function. Either function can be used because, where Q = 6, the supply and demand functions intersect – they have equal P values:
Demand price at Q=6: P = 10-1X6 = 10-6 = 4
Supply price at Q=6: P = 1+1/2X6 = 1+3 = 4
We have just solved a mathematical model of a particular market! It was not so difficult, but the method is very powerful and we will use it many times in the text.
In the demand and supply equations above the price appeared on the left hand side and quantity on the right. Normally this format implies a causation running from the right to the left hand side variable, while in economic markets we normally think of the quantity demanded and supplied depending upon the price in the market place. But the supply and demand equations can be rearranged so that quantity appears on the left and price on the right. For example the demand equation can be rewritten as follows:
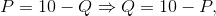
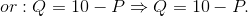
Writing the demand curve this way illustrates that the quantity intercept is 10 – the quantity demanded when the price becomes zero. The supply curve can be rearranged similarly.
- 瀏覽次數:1883






