Rentals are paid on an annual or per period basis. In order to relate rentals to the price of an asset it is necessary to determine the value in one period of the stream of rentals that an asset will earn over its life. In other words we need to find the present value of the stream of rental payments. This is done through discounting.
Imagine that you are promised the sum of $105 exactly one year from now. How would you value this today? The value today of $105 received a year from now is less than $105, because if you had this amount today you could invest it at the going rate of interest and end up with more than $105. For example, if the rate of interest is 5% (= 0.05), then $105 next year is equivalent to $100 today, because by investing the $100 today we would obtain an additional $5 at the end of the year. The amount returned to the investor is thus (one times) the original amount plus the interest rate times the amount. So, to obtain the next period value of a sum of money that we have today, we multiply this sum by one plus the rate of interest:
Value next period = value this period x (1 + interest rate)
By the same reasoning, to obtain the ‘today’ value of a sum obtained one year from now, that sum must be divided by one plus the interest rate. Dividing both sides of the above relation by (1+interest rate), and using the letter i to denote the interest rate:
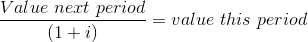
To push the example further: suppose you have $100 today and you want to find its value two years from now. In this case, the value of the $100 one year from now could be reinvested in total (the $100 plus the $5) to yield that sum multiplied by one plus the interest rate again:
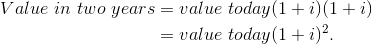
Correspondingly, the value today of a sum received in two years’ time is that sum divided by (1 + i) 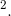 More generally the value today of any sum received t periods into the future is that sum divided by (1 + i)
More generally the value today of any sum received t periods into the future is that sum divided by (1 + i) 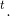
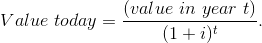
Note two features of this relationship. First, if the interest rate is high, the value today of future sums is smaller than if the interest rate is low. Second, sums received far in the future are worth much less than sums received in the near future: the denominator increases the larger is t.
Consider the example in Table
12.2 below: a machine earns $8,000 for each of two years. At the end of the second period the machine is almost ’dead’ and has a scrap value of $2,000. The interest rate is 10%. The present
value of each year’s income stream is given in the final column. The first payment is received in one year’s time, and therefore its value today is $8,000/(1.10)=$7,272.70. The value of the
second year’s income is $8;000/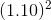 = $6,611.58. Finally the scrap
value is $2,000/
= $6,611.58. Finally the scrap
value is $2,000/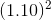 = $1,652.90. The present value of this future
income stream is simply the sum of these amounts is $15,537.18.
= $1,652.90. The present value of this future
income stream is simply the sum of these amounts is $15,537.18.
| Year | Annual earnings of machine $ | Scrap value $ | Discounted value $ |
| 1 | 8,000 | 7,272.70 | |
| 2 | 8,000 | 2,000 | 6,611.58 + 1,652.90 |
| Asset value in initial year | 15,537.18 | ||
| Interest rate = 10% | |||
 The present value of a stream of future earnings
is the sum of each year’s earnings divided by one plus the interest rate raised to the appropriate power.
The present value of a stream of future earnings
is the sum of each year’s earnings divided by one plus the interest rate raised to the appropriate power.
The value today of the services this machine offers should determine the price a buyer is willing to pay for the machine. If a potential buyer can purchase the machine for less than the present discounted value of the machine’s future earnings a potential buyer should purchase it. Conversely if the asking price for the machine exceeds the present value of the earnings, the potential buyer should avoid the purchase.
- 瀏覽次數:2043






