Land is an input used in production, though is not a capital good in the way we defined capital goods earlier – production inputs that are themselves produced in the economy. Land is relatively fixed in supply to the economy, even in the long run. While this may not be literally true – the Netherlands reclaimed from the sea a great quantity of low-lying farmland, and fertilizers can turn marginal land into fertile land – it is a good approximation to reality. Figure 12.9 shows the derived demand Do for land services. With a fixed supply S, the equilibrium rental is Ro.
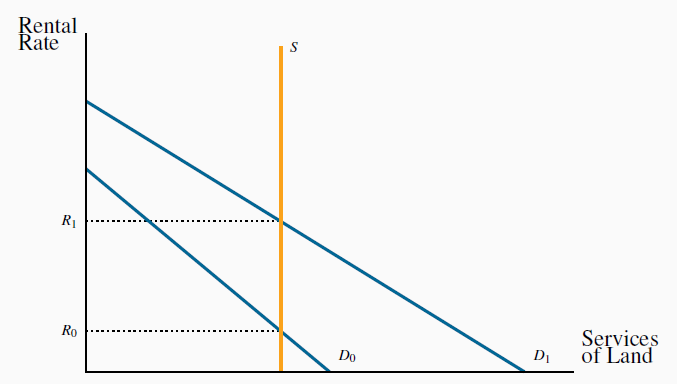
The supply of land is relatively fixed, and therefore the return to land is primarily demand determined. Shifts in demand give rise to differences in returns.
In contrast to this economy-wide perspective, consider now a retailer who rents space in a commercial mall. The area around the mall experiences a surge in development and more people are shopping and doing business there. The retailer finds that she sells more, but at the same time higher rents make it difficult for her to increase her profit. The reason why her profit may not increase greatly is that the demand for retail space is a derived demand: with growth in the surrounding area many more retailers would like to rent space at the previous rent. Accordingly, the market demand curve for rental space shifts upwards, and this in turn leads to an increase in the price of rental space.
Of course, land has many uses and the returns to land must reflect this. Land in downtown Vancouver is priced higher than land in rural Saskatchewan. Land cannot be moved from the latter to the former location however, and therefore the rent differences represent an equilibrium. In contrast, land in downtown Winnipeg that is used for a parking lot may not be able to compete with the use of that land for office development. Therefore, for it to remain as a parking lot, the rental must reflect its high opportunity cost. This explains why parking fees in big US cities such as Boston or New York may run to $40 per day. If the parking owners could not obtain this fee, they could profitable sell the land to a developer. Ultimately it is the value in its most productive use that determines the price of land.
KEY TERMS
Demand for labour: a derived demand, reflecting the demand for the output of final goods and services.
Value of the marginal product is the marginal product multiplied by the price of the good produced.
Marginal revenue product of labour is the additional revenue generated by hiring one more unit of labour where the marginal revenue declines.
Monopsonist is the sole buyer of a good or service and faces an upward-sloping supply curve.
Participation rate: the fraction of the population in the working age group that joins the labour force.
The labour force is that part of the population either employed or seeking employment.
Unemployment rate: the fraction of the labour force actively seeking employment that is not employed.
Transfer earnings are the amount that an individual can earn in the next highest paying alternative job.
Rent is the excess remuneration an individual currently receives above the next best alternative. This alternative is the reservation wage.
Gross investment is the production of new capital goods and the improvement of existing capital goods.
Net investment is gross investment minus depreciation of the existing capital stock.
Depreciation is the annual change in the value of a physical asset.
Stock is the quantity of an asset at a point in time.
Flow is the stream of services an asset provides during a period of time.
Capital services are the production inputs generated by capital assets.
Rental rate: the cost of using capital services.
Asset price: the financial sum for which the asset can be purchased.
Present value of a stream of future earnings: the sum of each year’s earnings divided by one plus the interest rate raised to the appropriate power.
EXERCISES
- Aerodynamics is a company specializing in the production of bicycle shirts. It has a fixed capital stock, and sells its shirts for $20 each. It pays a weekly wage of $400 per
worker. Aerodynamics must maximize its profits by determining the optimal number of employees to hire. The marginal product of each worker can be inferred from the table below. Determine the
optimal number of employees. [Hint: you must determine the VMPL schedule, having first computed the
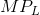 .]
.]
Employment 0 1 2 3 4 5 6 Total output 0 20 50 75 95 110 120 MPL VMPL - Mini Mine is a small mining firm in Northern Alberta. The going wage rate in the region is $300 per week. The productivity of the workers in the firm, which has a fixed
capital stock, is given below.
Workers 0 1 2 3 4 5 6 7 8 9 10 Output 0 100 190 270 340 400 450 490 520 540 550 MPL VMPL - If the price of ore is $10 per ton determine the optimal employment level for this firm.
- Instead of there being many potential workers, suppose that there are only 6 workers who can be hired in the neighbourhood. If the price of output is still fixed at $300,
and the productivity of workers is still defined by the data in the second row, draw the
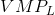 curve, insert the supply limit and determine the equilibrium wage.
curve, insert the supply limit and determine the equilibrium wage.
- Suppose that, in Question 1 above, wages are not fixed. Instead the firm must pay $50 more to employ each individual worker: the first worker is willing to work for $250, the second for $300, the third for $350, etc. But once employed, each worker actually earns the same wage. Determine the optimal number of workers to be employed. [Hint: you must recognize that each worker earns the same wage; so when one additional worker is hired, the wage must increase to all workers employed.]
- Consider the following supply and demand equations for berry pickers. Demand: W = 22 - 0.4L; supply: W = 10+0.2L.
- Plot these functions and calculate the equilibrium wage and employment level.
- Illustrate in the diagram the areas defining transfer earnings and rent.
- Compute the transfer earnings and rent components of the total wage bill.
- The industry demand in for plumbers is given by the equationW = 50 - 0.08L, and there is a fixed supply of 300 qualified plumbers.
- Draw a diagram illustrating the supply, demand and equilibrium.
- Solve the supply and demand equations for the equilibrium wage,W.
- If the plumbers now form a union, and supply their labour at a wage of $30 per hour, illustrate the new equilibrium on your diagram and calculate the new level of employment.
- The following table describes the income stream for different capital investments. The income flows accrue at the end of years 1 through 4. The interest rate is given in the
first column, and the cost in the final column.
Interest rate Year 1 Year 2 Year 3 Year 4 Cost 8% 8,000 9,000 12,000 12,000 37,000 6% 0 1,000 1,000 1,000 2,750 10% 4,000 5,000 6,000 0 12,000 - For each investment calculate the present value of the stream of services.
- Decide upon whether the investment should be undertaken or not.
- Nihilist Nicotine is a small tobacco farm in south-western Ontario. It has three plots of land, each with a different productivity. The output from each plot is given in the
table below. Each plot is the same size and requires 3 workers and one machine to harvest the leaves. The cost of these inputs is $10,000. If the price of each kilogram of leaves is $4, how
many fields should be planted?
Land plot Leaf yield in kilograms One 3,000 Two 2,500 Three 2,000 - The timing of wine sales is a frequent problem encountered by vintners. This is because many red wines improve with age. Let us suppose you own a particular vintage and you
envisage that each bottle should increase in value by 10% the first year, 9% the second year, 8% the third year, etc.
- Suppose the interest rate is 5%, for how many years would you hold the wine if there is no storage cost?
- If in addition to interest rate costs, there is a cost of storing the wine that equals 2% of the wine’s value each year, for how many years would you hold the wine before selling?
- A monopolist faces a demand curve given by P = 100 - 2Q. Labour is his only cost, and the wage rate is fixed at $8 per worker. Each worker has a constant marginal product
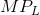 = 2, meaning that each additional worker produces two units of
output.
= 2, meaning that each additional worker produces two units of
output.
- The MC of each unit of output will be constant here, what is it?
- Since you now know the MC of production, what is the profit maximizing output level for the monopolist?
- What price will the monopolist charge for his output?
- How many units of labour will be employed?
- Suppose that instead of a monopolist in the previous question the market was perfectly competitive. Production conditions are the same.
- How much output would be produced and sold?
- How many units of labour would be employed?
- 2899 reads






