Imagine now that the good on the horizontal axis is charitable donations, rather than daycare, and the government decides that for every dollar given the individual will see a reduction in their income tax of 50 cents. This is equivalent to cutting the ‘price’ of donations in half, because a donation of one dollar now costs the individual half of that amount. Graphically the budget constraint rotates outward with the vertical intercept unchanged. Since donations now cost less the individual has increased spending power as a result of the price reduction for donations. The price reduction is designed to increase the attractiveness of donations to the utility maximizing consumer.
KEY TERMS
Cardinal utility is a measurable concept of satisfaction.
Total utility is a measure of the total satisfaction derived from consuming a given amount of goods and services.
Marginal utility is the addition to total utility created when one more unit of a good or service is consumed.
Diminishing marginal utility implies that the addition to total utility from each extra unit of a good or service consumed is declining.
Consumer equilibrium occurs when marginal utility per dollar spent on the last unit of each good is equal.
Law of demand states that, other things being equal, more of a good is demanded the lower is its price.
Ordinal utility assumes that individuals can rank commodity bundles in accordance with the level of satisfaction associated with each bundle.
Budget constraint defines all bundles of goods that the consumer can afford with a given budget.
Affordable set of goods and services for the consumer is bounded by the budget line from above; the non-affordable set lies strictly above the budget line.
Indifference curve defines combinations of goods and services that yield the same level of satisfaction to the consumer.
Indifference map is a set of indifference curves, where curves further from the origin denote a higher level of satisfaction.
Marginal rate of substitution is the slope of the indifference curve. It defines the amount of one good the consumer is willing to sacrifice in order to obtain a given
increment of the other, while maintaining utility unchanged.
Diminishing marginal rate of substitution reflects a higher marginal value being associated with smaller quantities of any good consumed.
Consumer optimum occurs where the chosen consumption bundle is a point such that the price ratio equals the marginal rate of substitution.
Substitution effect of a price change is the adjustment of demand to a relative price change alone, and maintains the consumer on the initial indifference curve.
Income effect of a price change is the adjustment of demand to the change in real income alone.
EXERCISES
- In the example given in Table 6.1, suppose Neal experiences a small increase in income. Will he allocate it to snowboarding or jazz? [Hint: At the existing equilibrium, which activity will yield the higher MU for an additional dollar spent on it?]
- Suppose that utility depends on the square root of the amount of good X consumed: U =
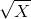 .
.
- In a spreadsheet enter the values 1. . . 25 in the X column, and in the adjoining column compute the value of utility corresponding to each quantity of X.
- In the third column enter the marginal utility (MU) associated with each value of X – the change in utility in going from one value of X to the next.
- Use the ‘graph’ tool to map the relationship between U and X.
- Use the graph tool to map the relationship between MU and X.
- Cappuccinos, C, cost $3 each, and music downloads of your favourite artist, M, cost $1 each from your iTunes store. Income is $24.
- Draw the budget line to scale, with cappuccinos on the vertical axis, and compute its slope.
- If the price of cappuccinos rises to $4, compute the new slope.
- At the initial set of prices, are the following combinations of goods in the affordable set: (4C and 9M), (6C and 2M), (3C and 15M)?
- Which combination(s) in part (c) lie inside the affordable set, and which lie on the boundary?
- George spends his income on gasoline and “other goods.”
- First, draw a budget constraint, with gasoline on the horizontal axis. Then, illustrate by how much the intercept on the gasoline axis changes in response to a doubling of the price of gasoline.
- Suppose that, in addition to a higher price, the government imposes a ration on George that limits his purchase of gasoline to less than some amount within his affordable set. Draw the new effective budget constraint.
- Instead of the ration in the preceding question, suppose that the government increases taxes on gasoline, in addition to the market price increase. Illustrate this budget constraint.
- The price of cappuccinos is $3, the price of a theatre ticket is $12, and consumer income is $72.
- In a graph with theatre tickets on the vertical axis and cappuccinos on the horizontal axis, draw the budget constraint to scale, marking the intercepts.
- Suppose the consumer chooses the combination of 4 theatre tickets and 8 cappuccinos. Draw such a point on the budget constraint and mark the affordable and non-affordable regions.
- Is the combination of 3 tickets and 24 cappuccinos affordable?
- (d) Is the combination in part (c) preferred to, or less preferred than, the chosen point in part (b)?
- If the price of cappuccinos falls to $2 per cup, is the combination of 24 cappuccinos and 3 tickets affordable?
- Suppose that you are told that the indifference curves defining the trade-off for two goods took the form of straight lines. Which of the four properties outlines in Choice with ordinal utility would such indifference curves violate?
- A student’s income is $50. Lunch at the cafeteria costs $5, and movies at the Student Union cost $2 each.
- Draw the budget line to scale, with lunch on the vertical axis; insert some regularshaped smooth convex indifference curves, and choose the tangency equilibrium, denoted
by
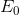 .
.
- If the price of lunch falls to $2.50, draw the new budget line. What can be said about the new equilibrium relative to
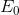 if both goods are normal?
if both goods are normal?
- If the price of movies also falls to $1, draw the new budget line and illustrate a new equilibrium.
- How does the equilibrium in part (c) differ from the equilibrium in part (b)?
- Draw the budget line to scale, with lunch on the vertical axis; insert some regularshaped smooth convex indifference curves, and choose the tangency equilibrium, denoted
by
- Lionel likes to eat a nice piece of Brie cheese while having a glass of wine. He has a monthly gourmet budget of $120. In a diagram with wine on the vertical axis and cheese
on the horizontal axis, suppose that the intercepts are 10 bottles on the wine axis and 4 kilos on the cheese axis. He is observed to purchase 5 bottles of wine and 2 kilos of cheese.
- What are the prices of wine and cheese?
- Suppose that the price of wine increases to $20 per bottle, but that LionelŠs income simultaneously increases by $60. Draw the new budget constraint and mark the intercepts.
- Is Lionel better off in the new or old situation? [Hint: ask if he can now afford the bundle he purchased with a lower income and lower wine price.]
- An indifference curve is a relationship between two goods, X and Y, such that utility is constant. Consider the following indifference curve: Y = 12/X. Since this can also be
written as 12 = XY then we can think of the value 12 as representing the utility level.
- In a spreadsheet enter the values 1. . . 24 in the X column, and in the adjoining Y column compute the value of Y corresponding to each value of X.
- Use the graph function to map this indifference curve.
- Compute the MRS where X increases from 3 to 4, and again where it increases from 15 to 16. [Hint: Since the MRS is the change in the amount of Y that compensates for a change in the amount of X, you need simply calculate the changes in Y corresponding to each of these changes in X.]
- Draw an indifference map with several indifference curves and several budget constraints corresponding to different possible levels of income. Note that these budget constraints should all be parallel because only income changes, not prices. Now find some optimizing (tangency) points. Join all of these points. You have just constructed what is called an income-consumption curve. Can you understand why it is called an income-consumption curve?
- Draw an indifference map again, in conjunction with a set of budget constraints. This time the budget constraints should each have a different price of good X and the same
price for good Y.
- Draw in the resulting equilibria or tangencies and join up all of these points. You have just constructed a price-consumption curve for good X. Can you understand why the curve is so called?
- Now repeat part (a), but keep the price of X constant and permit the price of Y to vary. The resulting set of equilibrium points will form a price consumption curve for good Y.
- From the equilibrium based on the data in Table 6.1, let us compute some elasticities, using the midpoint formula that we developed in Chapter 4. Suppose that the price of jazz falls to $16 per outing, from the
initial price of $20. Income remains at $200.
- First compute Neal’s new equilibrium – by computing a new MU/P schedule for jazz and reallocating his budget in a utility-maximizing fashion.
- What is his price elasticity of demand for jazz at this set of prices? [Hint: Once you compute the new quantity of jazz purchased you can compute the percentage change in quantity demanded. You also know the percentage change in the price of jazz, so you can now compute the ratio of these two numbers.]
- What is the cross-price elasticity of demand for snowboarding, with respect to the price of jazz, at this set of prices? [Hint: Calculate the percentage change in the number of snowboard visits to Whistler, relative to the percentage change in the price of jazz.]
- Suppose that movies are a normal good, but public transport is inferior. Draw an indifference map with a budget constraint and initial equilibrium. Now let income increase and draw a plausible new equilibrium, noting that one of the goods is inferior.
- Consider the set of choices facing the consumer in Figure 6.12, Figure 6.13, and Figure 6.14. The parent chooses between other goods and daycare.
- First, replicate this figure with one budget constraint and one indifference curve that together define a tangency (equilibrium) solution.
- Suppose now that daycare is subsidized through a price reduction. Draw two possible equilibria, one where “other goods” purchased increase, and the second where they decrease. In which case are daycare and other goods substitutes? In which case are they complements?
- 瀏覽次數:3350






