Truth tables and equivalences are useful and powerful tools, but they do not correspond to how we usually reason about things. What we will do now is look at more familiar reasoning and how to formalize that. For example, with Boolean algebra it is awkward to prove that a ∧ b implies a. For that, it is necessary to reword the problem in terms of equivalences, as a ∧ b ⇒ a ≡ true. Our next tool provides a more straightforward way to reason about implications.
Example 2.11
Given the following piece of a WaterWorld board, how would you conclude that G is unsafe?
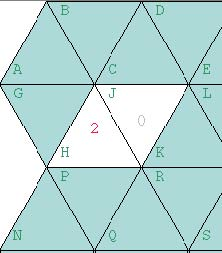
Since H− has − 2, at least two of H's three neighbors must be unsafe. But, since we know that one of these, J, isn't unsafe, then the two others, including G, must both be unsafe. Let's write this out more explicitly:
|
1 |
H - has - 2would imply one of the following is true: (P - unsafe and G - unsafe), or (J - unsafe and P - unsafe), or (G - unsafe and J - unsafe). |
WaterWorld domain axiom, i.e., definition of H - has - 2 |
|
2 |
H - has - 2 is true. |
Premise (by inspection of this particular board) |
|
3 |
One of the following is true: (P - unsafe and G - unsafe), or (J - unsafe and P - unsafe), or (G - unsafe and J - unsafe). |
lines 1,2 |
|
4 |
not J - unsafe |
Premise (by inspection) |
|
5 |
(P - unsafe and G - unsafe) |
lines 3,4 |
|
6 |
G - unsafe |
line 5 |
Whew! A lot of small steps are involved in even this small deduction. It's apparent we'd want to automate this as much as possible! Let's look at some other short examples, which we'll formalize in a moment.
Exercise 2.4.1.1
How do you know that A − has − 2 proves B − unsafe ?
Exercise 2.4.1.2
Similarly, how do you reason that A − has − 1 and G − safe prove B − unsafe?
- 3719 reads






