In the above examples, we relied on common sense to know what new true formulas could be derived from previous ones. Unfortunately, common sense is imprecise and sometimes wrong. So, we need to formalize how we form proofs.
We now define a formal proof of θ from the premises φ, ..., ψ, written
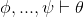
(A proof with no premises simply means there is nothing on the left of the turnstile: 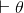 .) For example, we'll show shortly that H − has − 2 f G − unsafe. A proof consists of a sequence of
WFFs, each with a justifcation for its truth. We will describe four permissible justifcations for each step:
.) For example, we'll show shortly that H − has − 2 f G − unsafe. A proof consists of a sequence of
WFFs, each with a justifcation for its truth. We will describe four permissible justifcations for each step:
- A premise.
- An axiom.
- An inference rule.
- A subproof.
ASIDE: Ofcially we might want to annotate the turnstile with "ww", to mean "proves within the WaterWorld inference system", indicating our use of the WaterWorld domain axioms. If you're proving things about other domains, you'd use different domain axioms.
Example 2.12
We can formalize the above examples to show each of the following:
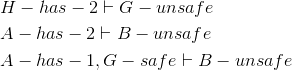
See below for formal proofs of some of these.
Stating an axiom, a simple assumed truth, is a rather trivial, boring way of coming up with a true formula. Some axioms are domain axioms: they pertain only to the domain you are considering, such as WaterWorld. In our case, we don't have any axioms that aren't domain axioms. If our domain were arithmetic, our axioms would describe how multiplication distributes over addition, etc.
Just using axioms is not enough, however. The interesting part is to deduce new true formulas from axioms and the results of previous deductions.
An inference rule formalizes what steps are allowed in proofs. We'll use this list of valid inference rules (Propositional inference rules) as our defnition, but, this is just one set of possible inference rules, and other people could use slightly different ones.
First, let's look at some simple examples, using the simpler inference rules.
Example 2.13
We'll formalize a previous exercise (Exercise 2.4.1.1) to show 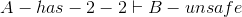 .
.
|
1 |
A – has – 2 |
Premise |
|
2 |
A – has – 2 ⇒ B – unsafe ∧ F - unsafe |
WaterWorld domain action |
|
3 |
B – unsafe ∧ F – unsafe |
⇒Elim, lines 1,2, where ψ = A – has – 2, and φ = B – unsafe ∧ F - unsafe |
|
4 |
B – unsafe |
∧Elim (left), line 3, where ψ = B – unsafe, and φ = F - unsafe |
What we mean in line 3, for example, is that we are using the domain axiom ⇒Elim. That states that if we know φ ⇒ ψ, and we know φ, then we can conclude ψ. In line 3, we have defined φ = A − has − 2 and ψ =B − unsafe ∧ F − unsafe, so that φ ⇒ ψ corresponds to the conclusion of line 2 and φ corresponds to that of line 1. Thus, this domain axiom applies, and we get the conclusion ψ.
That's almost exactly like the steps we took in the previous informal proof, but now we're a bit pickier about our justifcations for each step.
Formally, when using a domain axiom, the justifcation is a combination of the name of that inference rule, the line numbers of which previous WFFs are being used, and a description of how those WFFs are used in that inference rule in this particular step. Later, we'll often omit the description of exactly how the specifc inference rule is used, since in many cases, that information is painfully obvious.
Example 2.14
In this system, commutativity of ∧ and ∨ are not among the inference rules. However, they do follow. For example, consider the following proof of
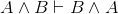
|
1 |
A ∧ B |
Premise |
|
2 |
A |
∧Elim (left), line 1, where φ = A |
|
3 |
B |
∧Elim (right), line 1, where ψ = B |
|
4 |
B ∧ A |
∧Intro, lines 3,2, where φ = B, and ψ = A |
Does this example (Example 2.14) also show that 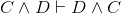 ? Well, yes
and no. That proof does not have anything to do with propositions C and D. But, clearly, we could create another
nearly identical proof for
? Well, yes
and no. That proof does not have anything to do with propositions C and D. But, clearly, we could create another
nearly identical proof for 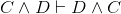 , by substituting
C and D for A and B, respectively. What about proving the other direction of
commutativity:
, by substituting
C and D for A and B, respectively. What about proving the other direction of
commutativity: 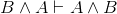 ? Once again, the proof has exactly the same
form, but substituting B and A for A and B, respectively. Stating such similar proofs
over and over is technically necessary, but not very interesting. Instead, when the proof depends solely on the form of the formula and not on any axioms, we'll use meta-variables to
generalize.
? Once again, the proof has exactly the same
form, but substituting B and A for A and B, respectively. Stating such similar proofs
over and over is technically necessary, but not very interesting. Instead, when the proof depends solely on the form of the formula and not on any axioms, we'll use meta-variables to
generalize.
Example 2.15
Generalized ∧ commutativity:
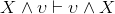
|
1 |
χ∧υ |
Premise |
|
2 |
υ |
∧Elim (left), line 1, where φ =χ |
|
3 |
χ |
∧Elim (right), line 1, where ψ =υ |
|
4 |
υ ∧ χ |
∧Intro, lines 3,2, where φ = υ, ψ=χ |
Exercise 2.4.1.3
Similarly, associativity of ∧ and ∨ are not among the inference rules. This is a particularly important detail, since our WaterWorld domain axioms frequently use formulas of the form
a ∧ b ∧ c, which isn't technically legal according to our definition of WFFs. What we'd like to show is that 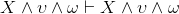 and
and 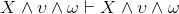 as well as the
equivalent for ∨. Thus, when we see three, four, or more terms in a conjunction (or disjunction), we can legitimately group them as we see fit.
as well as the
equivalent for ∨. Thus, when we see three, four, or more terms in a conjunction (or disjunction), we can legitimately group them as we see fit.
These deductions are straightforward and should be unsurprising, but perhaps not too interesting. These simple rules can carry us far and will be used commonly in other examples.
Example 2.16
The case-elimination rule is easy enough for a dog! Rico has a vocabulary of over 200 words, and if asked to fetch an unknown toy, he can pick it out of a group of known toys by process-of-elimination. (It's almost enough to make you wonder whether dogs know calculus.)

There is a subtle difference between implication (⇒) and provability (f). Both embody the idea that the truth of the right-hand-side follows from the left-hand-side. But, ⇒ is a syntactic formula connective combining two WFFs into a larger WFF, while f combines a list of propositions and a WFF into a statement about provability.
Exercise 2.4.1.4
Show that, 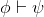 is equivalent to
is equivalent to 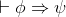 in that, we can show one if and only if we can show the other.
in that, we can show one if and only if we can show the other.
- 4689 reads






