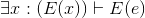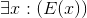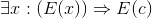Exercise 4.4.28
Prove that syllogisms are valid inferences. In other words, show that ∀x :
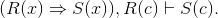
Exercise 4.4.29
What is wrong with the following "proof" of ∃x :(E (x)) ⇒ E (c)?
|
1 |
subproof: |
||
|
1.a |
|
Premise for subproof |
|
|
1.b |
E (c) |
∃Elim, line 1.a |
|
|
2 |
|
⇒Intro, line 1 |
|
Exercise 4.4.30
Using the inference rules, formally prove the last part of the previous problem about ducks and such (Exercise 4.4.11).
Exercise 4.4.31
Give an inference rule proof of ∀x : (Fruit (x) ⇒ hasMethod (tast y,x)) , ∀y : (Apple
(y) ⇒ Fruit (y)) 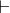 ∀z : (Apple
(z) ⇒ hasMethod (tast y,z)).
∀z : (Apple
(z) ⇒ hasMethod (tast y,z)).
Exercise 4.4.32
- Prove the following: ∃x :(P (x))
, ∀y :(P (y) ⇒ Q
(y))
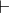 ∃z :(Q (z))
∃z :(Q (z))
- Your proof above used ∃Intro. Why can't we replace that step with the formula ∀z :(Q (z)) with the justification "∀Intro"?
- Describe an interpretation which satisfies the proof's premises, but does not satisfy ∀z : (Q (z)).
- 3815 reads