You are here

Home » Intro to Logic » First-Order Logic » Exercises for First-Order Logic

Reasoning with Equivalences

23 July, 2015 - 12:53
Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/383d4b87-2d7b-454e-99fe-2eaa43eae8ff@20.20

Exercise 4.4.24

Some of the first-order equivalences (First-order equivalences) are redundant. For each of the following, prove the equivalence using the other equivalences.

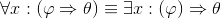
  1. \forall x:(\varphi \Rightarrow \theta)\equiv \exists x:(\varphi )\Rightarrow \theta
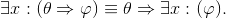
  2. Assuming a non-empty domain, \exists x:(\theta \Rightarrow \varphi )\equiv \theta \Rightarrow \exists x:(\varphi ).

Exercise 4.4.25

We can characterize a prime number as a number n satisflying 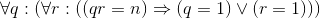\forall q:(\forall r:((qr=n)\Rightarrow (q=1)\vee (r=1))). Using the equivalences for first-order logic, show step-by-step that this is equivalent to the formula 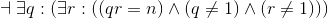\dashv \exists q:(\exists r:((qr=n)\wedge (q\neq 1)\wedge (r\neq 1))). Do not use any arithmetic equivalences.

Exercise 4.4.26

A student claims that 

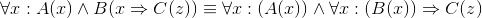
\forall x:A(x)\wedge B(x\Rightarrow C(z))\equiv \forall x:(A(x))\wedge \forall x:(B(x))\Rightarrow C(z)
by the "distribution of quantifiers". This is actually trying to do two steps at once. Rewrite this as the two separate intended steps, determine which is wrong, and describe why that step is wrong.

Exercise 4.4.27

Simplify the formula 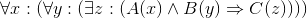\forall x:(\forall y:(\exists z:(A(x)\wedge B(y)\Rightarrow C(z)))), so that the body of each quantifier contains only a single atomic formula (Definition : "Well-Formed Formula (WFF) for first-order logic") involving that quantified variable. Provide reasoning for each step of your simplification.

  • 3179 reads