The following equivalences are in addition to those of propositional logic (Propositional equivalences). In these, φ and ψ each stand for any WFF, but θ stands for any WFFwith no free occurrences of x .
|
Equivalence |
∀ Variant |
∃ Variant |
|---|---|---|
|
Complementation of Quantifiers |
∀x : (¬φ) ≡ ¬∃x : (φ) |
∃x : (¬φ) ≡ ¬∀x : (φ) |
|
Interchanging Quantifiers |
∀x : (∀y : (φ)) ≡ ∀y : (∀x : (φ)) |
∃x : (∃y : (φ)) ≡ ∃y : (∃x : (φ)) |
|
Distribution of Quantifiers |
∀x : (φ ∧ ψ) ≡ ∀x : (φ) ∧ ∀x : (ψ) |
∃x : (φ ∨ ψ) ≡ ∃x : (φ) ∨ ∃x : (ψ) |
|
∀x : (φ ∨ θ) ≡ ∀x : (φ) ∨ θ |
∃x : (φ ∧ θ) ≡ ∃x : (φ) ∧ θ |
|
|
∀x : (φ ⇒ θ) ≡ ∃x : (φ) ⇒ θ |
||
|
∀x : (θ ⇒ φ) ≡ θ ⇒ ∀x : (φ) |
||
|
Distribution of Quantifiers − − − with non-empty domain |
∀x : (φ ∧ θ) ≡ ∀x : (φ) ∧ θ |
∃x : (φ ∨ θ) ≡ ∃x : (φ) ∨ θ |
|
∃x : (φ ⇒ θ) ≡ ∀x : (φ) ⇒ θ |
||
|
∃x : (θ ⇒ φ) ≡ θ ⇒ ∃x : (φ) |
||
|
Renaming |
∀x : (φ) ≡ ∀y : (φ [x → y]) |
∃x : (φ) ≡ ∃y : (φ [x → y]) |
|
Simplification of Quantifiers − − − with non-empty domain |
∀x : (θ) ≡ θ |
∃x : (θ) ≡ θ |
|
Simplification of Quantifiers − − − with empty domain |
∀x : (φ) ≡ true |
∃x : (φ) ≡ false |
When citing Distribution of Quantifiers, say what you're distributing over what: e.g., " distribute ∀ over ∨ (with θ being x-free) ".
In renaming, the notation φ [x → y] means " φ with each free occurrence of x replaced by y ". It is a meta-formula; when writing any particular formula you don't write any brackets, and instead just do the replacement.
This set of equivalences isn't actually quite complete. For instance,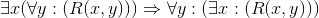 
is equivalent to true, but we can't show it using only the rules above. It does become complete5 if we
add some analogs of the First-order inference rule, replacing 
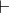with ⇒ (and carrying along their baggage of "arbitrary" and "free-to-substitute-in").
- 1686 reads
