Economies of scope refers to the possibility that it may be less expensive to produce and sell a line of related goods than to produce just one product from such a line. Scope economies, therefore, define the returns or cost reductions associated with broadening a firm’s product range.
Corporations like Proctor and Gamble do not produce a single product in their health line; rather, they produce first aid, dental care, and baby care products. Cable companies offer their customers TV, high-speed Internet, and voice-over telephone services either individually or packaged.
 Economies of scope occur if the unit cost of
producing particular products is less when combined with the production of other products than when produced alone.
Economies of scope occur if the unit cost of
producing particular products is less when combined with the production of other products than when produced alone.
KEY TERMS
Production function: a technological relationship that specifies how much output can be produced with specific amounts of inputs.
Technological efficiency means that the maximum output is produced with the given set of inputs.
Economic efficiency defines a production structure that produces output at least cost.
Short run: a period during which at least one factor of production is fixed. If capital is fixed, then more output is produced by using additional labour.
Long run: a period of time that is sufficient to enable all factors of production to be adjusted.
Very long run: a period sufficiently long for new technology to develop.
Total product is the relationship between total output produced and the number of workers employed, for a given amount of capital.
Marginal product of labour is the addition to output produced by each additional worker. It is also the slope of the total product curve.
Law of diminishing returns: when increments of a variable factor (labour) are added to a fixed amount of another factor (capital), the marginal product of the variable factor
must eventually decline.
Average product of labour is the number of units of output produced per unit of labour at different levels of employment.
Fixed costs are costs that are independent of the level of output.
Variable costs are related to the output produced.
Total cost is the sum of fixed cost and variable cost.
Average fixed cost is the total fixed cost per unit of output.
Average variable cost is the total variable cost per unit of output
Average total cost is the sum of all costs per unit of output.
Marginal cost of production is the cost of producing each additional unit of output.
Sunk cost is a fixed cost that has already been incurred and cannot be recovered, even by producing a zero output.
Increasing returns to scale implies that, when all inputs are increased by a given proportion, output increases more than proportionately.
Constant returns to scale implies that output increases in direct proportion to an equal proportionate increase in all inputs.
Decreasing returns to scale implies that an equal proportionate increase in all inputs leads to a less than proportionate increase in output.
Long-run average total cost is the lower envelope of all the short-run ATC curves.
Minimum efficient scale defines a threshold size of operation such that scale economies are almost exhausted.
Long run marginal cost is the increment in cost associated with producing one more unit of output when all inputs are adjusted in a cost minimizing manner.
Technological change represents innovation that can reduce the cost of production or bring new products on line.
Globalization is the tendency for international markets to be ever more integrated.
Cluster: a group of firms producing similar products, or engaged in similar research.
Learning by doing can reduce costs. A longer history of production enables firms to accumulate knowledge and thereby implement more efficient production processes.
Economies of scope occur if the unit cost of producing particular products is less when combined with the production of other products than when produced alone.
EXERCISES
- Suppose you are told by a production engineer that the relationship between output Q on the one hand and input, in the form of labour (L), on the other is Q = 5
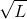 . Capital is fixed, so we are operating in the short run.
. Capital is fixed, so we are operating in the short run.
- Compute the output that can be produced in this firm using 1 through 9 units of labour by substituting these numbers into the production function.
- Draw the resulting TP curve to scale, relating output to labour.
- Inspect your graph to see that it displays diminishing MP.
- The total product schedule for Primitive Products is given in the table below.
Output 1 6 12 20 30 42 53 60 66 70 Labour 1 2 3 4 5 6 7 8 9 10 - Draw the total product function for this firm to scale, or by using a spreadsheet.
- Calculate the AP and draw the resulting relationship on a separate graph.
- Calculate the MP and draw the schedule on the same graph as the AP.
- By inspecting the AP and MP curves, can you tell if you have drawn them correctly? Why?
- Return to Question 1 above and now calculate and plot the AP and MP curves.
- A short-run relationship between output and total cost is given in the table below.
Output 0 1 2 3 4 5 6 7 8 9 Total Cost 12 27 40 51 61 70 80 91 104 120 - What is the total fixed cost of production in this example?
- Add some rows to your table and calculate the AFC, AVC, and ATC curves for each level of output.
- Calculate the MC of producing additional levels of output.
- Graph each of these four cost curves using the information you have developed.
- Bernie’s Bagels can function with three different oven capacities. For any given amount of labour, a larger output can be produced with a larger-capacity oven. The cost of a
small oven is $100; the cost of a medium-sized oven is $140; and the cost of a large oven is $180. Each worker is paid $60 per shift. The production levels for each plant size are given in
the table below.
Labour Small-oven output Med-oven output Large-oven output 1 15 20 22 2 30 40 46 3 48 64 70 4 56 74 80 - Compute and graph AP and MP curves for each size of operation.
- Verify that the relationship between the AP and MP curves is as it should be.
- Now consider the cost curves associated with the production functions in the preceding question.
- Compute the ATC schedule for the medium plant size and verify that it is U shaped.
- Now consider the preceding question in the longer term – with variable plant size.
- Compute the ATC for the small plant and large plant.
- By inspecting all three ATC curves, what can you say about scale economies over the range of output being considered?
- The table below defines the inputs required in the long run to produce three different output levels using different combinations of capital and labour. The cost of labour is
$5 and the cost of capital is $2 per unit.
Capital used 4 2 7 4 11 8 Labour used 5 6 10 12 15 16 Output 4 4 8 8 12 12 - Calculate the least-cost method of producing each of the three levels of output defined in the bottom row.
- On a graph with cost on the vertical axis and output on the horizontal axis, plot the relationship you have calculated in between cost per unit and output. You have now plotted the long-run average cost.
- Suppose now that the cost of capital in the previous question rises to $3 per unit. Graph the new long-run average cost curve, and compare its position with the curve in that question.
- Consider the long-run total cost structure for the following two firms.
Output 1 2 3 4 5 6 7 Firm A $40 $52 $65 $80 $97 $119 $144 Firm B $30 $40 $50 $60 $70 $80 $90 - Compute the long-run ATC curve for each firm.
- Plot these curves and examine the type of scale economies each firm experiences at different output levels.
- Use the data in the preceding question to establish the LMC for each of these two firms.
- Check that these LMC curves intersect with the LAC curves appropriately.
- 1Consider a firm whose ATC (in the short run) is given by: ATC = 2/Q+1+Q/8.
- Using a spreadsheet plot this curve for values of output in the range 1. . . 20. You should first compute the cost values in a table.
- Next tabulate the total cost for each level of output, using the fact that total cost is the product of quantity times ATC.
- Now compute the marginal cost in the fourth column of your table by observing how total cost changes at each level of output.
- Plot the MC curve on the same graph as the ATC curve, and verify that it cuts the ATC at its minimum point.
- Suppose you are told that a firm has a long run average total cost that is defined by the following relationship: LATC = 4+48/Q.
- Plot this curve for several values of Q in the range 1. . . 24.
- What kind of returns to scale does this firm never experience?
- By examining your graph of the LATC curve, what will be the numerical value of the ATC as output becomes very large?
- Can you guess what the form of the LMC curve is?
- 瀏覽次數:3266






