We have now come full circle. We started this chapter by describing the key role in economic development and growth played by firms and capital markets. Capital markets channel the funds of individual investors to risk-taking firms. Such firms—whether they are Dutch spice importers in the seventeenth century, the Hudson’s Bay Company in nineteenth-century Canada, companies in Alberta’s tar sands today or high tech start-ups in Silicon Valley—are engines of growth and play a pivotal role in an economy’s development. Capital markets are what make it possible for these firms to attract the savings of risk-averse individuals. By enabling individuals to diversify their portfolios, capital markets form the link between individuals and firms.
We next turn to examine decision making within the firm. Firms must make the right decisions if they are to grow and provide investors with a satisfactory return. These producers bringing a product to market are the survivors of the uncertainty surrounding product development.
KEY TERMS
Sole proprietor is the single owner of a business and is responsible for all profits and losses.
Partnership: a business owned jointly by two or more individuals, who share in the profits and are jointly responsible for losses.
Corporation or company is an organization with a legal identity separate from its owners that produces and trades.
Shareholders invest in corporations and therefore are the owners. They have limited liability personally if the firm incurs losses.
Dividends are payments made from after-tax profits to company shareholders.
Capital gains (losses) arise from the ownership of a corporation when an individual sells a share at a price higher (lower) than when the share was purchased.
Limited liability means that the liability of the company is limited to the value of the company’s assets.
Retained earnings are the profits retained by a company for reinvestment and not distributed as dividends.
Principal or owner: delegates decisions to an agent, or manager.
Agent: usually a manager who works in a corporation and is directed to follow the corporation’s interests.
Principal-agent problem: arises when the principal cannot easily monitor the actions of the agent, who therefore may not act in the best interests of the principal.
Stock option: an option to buy the stock of the company at a future date for a fixed, predetermined price.
Fair gamble: one where the gain or loss will be zero if played a large number of times.
Risk: the risk associated with an investment can be measured by the dispersion in possible outcomes. A greater dispersion in outcomes implies more risk. 192
Risk-averse person will refuse a fair gamble, regardless of the dispersion in outcomes.
Risk-neutral person is interested only in whether the odds yield a profit on average, and ignores the dispersion in possible outcomes.
Risk pooling: a means of reducing risk and increasing utility by aggregating or pooling multiple independent risks.
Risk spreading: spreads the risk of a venture among multiple sub insurers.
Real return: the nominal return minus the rate of inflation.
Real return on corporate stock: the sum of dividend plus capital gain, adjusted for inflation.
Capital market: a set of financial institutions that funnels financing from investors into bonds and stocks.
Portfolio: a combination of assets that is designed to secure an income from investing and to reduce risk.
Diversification reduces the total risk of a portfolio by pooling risks across several different assets whose individual returns behave independently.
Variance is the weighted sum of the deviations between all possible outcomes and the mean, squared.
EXERCISES
- Estimate the average dollar outcome of each of the following games. Each dollar outcome has a probability of one-quarter. Then compute the average utility associated with each
game, given the utility values that are associated with each dollar outcome.
- $12,000,U = 109.5;$11,000,U = 104.9;$9,000,U = 94.9;$8,000;U = 89.4.
- $32,000,U = 178.9;$31,000,U = 176.1;$29,000,U = 170.3;$28,000,U = 167.3.
- $24,000,U = 154.9;$22;000,U = 148.3;$18,000,U = 134.2;$16,000,U = 126.5.
- You see an advertisement for life insurance for everyone 50 years of age and older. No medical examination is required. If you are a healthy 52-year old, do you think you will get a good deal from this company?
- In which of the following are risks being pooled, and in which would risks likely be spread by insurance companies?
- Insurance against Alberta’s Bow River Valley flooding.
- Life insurance.
- Insurance for the voice of Avril Lavigne or Celine Dion.
- Insuring the voices of the lead vocalists in Metallica, Black Eyed Peas, Incubus, Evanescence, Green Day, and Jurassic Five.
-
- Plot the following three utility functions that relate utility U to wealthW, for values of wealth in the range 1. . . 50, using a spreadsheet tool such as
Excel:
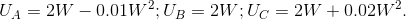
- State whether each utility function displays risk neutrality, risk aversion or risk love.
- Judging from the shapes of the functions you have plotted, do they display increasing, constant or diminishing marginal utility?
- Plot the following three utility functions that relate utility U to wealthW, for values of wealth in the range 1. . . 50, using a spreadsheet tool such as
Excel:
- Use the data in Table 7.2 to
compute the average utility that each participant gets from his or her income in the different situations under the following assumption about utility: with no pooling of risk, the utilities
are either from obtaining $5000 or from obtaining zero. But, with risk pooling, there is also the possibility of getting the utility associated with an income of $2500. Suppose that the
utility from getting a zero income is zero, the utility from $2500 is 50, and the utility from $5000 is 70.7.
- How much more utility will each individual get, on average, when sharing his or her income with their partner relative to when not sharing?
- In the example developed in Table 7.3, suppose there are four identical firms with the same return pattern, and the investor again has $200 to invest.
- Compute the portfolio variance associated with a strategy of investing $50 in each stock. To do this you can use a property of the variance of a portfolio: when the stock prices move independently, the variance of the portfolio of stocks is the sum of the variance of each stock. So compute the variance of each stock, where $50 is invested in each, and the variance of the portfolio will be four times this amount.
- A worker has a utility of income function defined by U =
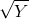 .
.
- Plot this utility function for values of income in the range 1. . . 36.
- Suppose the individual this time period has Y = 16, and he has a 50% chance of seeing his income increase or decrease. If it decreases we know it will fall to $1. If it increases, by how much would income have to increase to leave his expected utility equal to the level he attains when he gets an income of $16 with certainty?
- Once again consider a worker who has a utility function U =
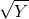 . In a good week he earns $25 and in a bad week he earns nothing. Good and bad weeks each have probabilities of 50%.
. In a good week he earns $25 and in a bad week he earns nothing. Good and bad weeks each have probabilities of 50%.
- What is his average or expected utility in numerical terms?
- Suppose the government enters the picture and requires him to contribute to an unemployment insurance scheme. He must pay $9 every time he has a good week. In return the government pays him $9 whenever he has a bad week. Compute his average or expected utility with the new insurance scheme in place.
- Consider the individual in the preceding question once again. He earns either zero or $25 with equal probability in every time period. There is no employment insurance scheme.
- If this individual thinks about the fact that he may be unemployed in any time period, how much should he save every (good) time period in order to have the maximum average or expected utility over time?
- Suppose an individual has utility that increases with the log of his wealth: U =ln(W), where W is a number that denotes wealth. Compute the value of U for values of W running from 1. . . 20 (not including zero). Then plot the graph of the function and determine if it displays increasing, constant or decreasing marginal utility.
- 瀏覽次數:3773






