The cost structure for the production of snowboards at Black Diamond is illustrated in Table 8.2. Employees are skilled and are paid a weekly wage of $1000. The cost of capital is $3000 and it is fixed, which means that it does not vary with output. As in Table 8.2, the number of employees and the output are given in the first two columns. The following three columns define the capital costs, the Labour costs, and the sum of these in producing different levels of output. We use the terms fixed, variable, and total costs to define the cost structure of a firm. Fixed costs do not vary with output, whereas variable costs do, and total costs are the sum of fixed and variable costs.
 Fixed costs are costs that are independent of the
level of output.
Fixed costs are costs that are independent of the
level of output.
 Variable costs are related to the output produced.
Variable costs are related to the output produced.
 Total cost is the sum of fixed cost and variable
cost.
Total cost is the sum of fixed cost and variable
cost.
Total costs are illustrated in Figure 8.3 as the vertical sum of variable and fixed costs. For example, Table 8.2 indicates that the total cost of producing 220 units of output is the sum of $3000 in fixed costs plus $8000 in variable costs. Therefore, at the output level 220 on the horizontal axis in Figure 8.3, the sum of the cost components yields a value of $11,000 that forms one point on the total cost curve. Performing a similar calculation for every possible output yields a series of points that together form the complete total cost curve.
Average costs are given in the next three columns of Table 8.2. Average cost is the cost per unit of output, and we can define an average cost corresponding to each of the fixed, variable, and total costs defined above. Average fixed cost (AFC) is the total fixed cost divided by output; average variable cost (AVC) is the total variable cost divided by output; and average total cost (ATC) is the total cost divided by output.
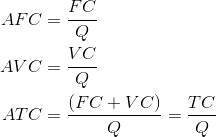
 Average fixed cost is the total fixed cost per
unit of output.
Average fixed cost is the total fixed cost per
unit of output.
 Average variable cost is the total variable cost
per unit of output.
Average variable cost is the total variable cost
per unit of output.
 Average total cost is the sum of all costs per
unit of output.
Average total cost is the sum of all costs per
unit of output.
The average variable cost is given in column 7 of Table 8.2, and a corresponding curve is plotted in Figure 8.4. In this example, AVC first decreases and then increases. The intuition behind its shape is straightforward (and realistic) if you have understood why productivity varies in the short run: The cost of employing each additional worker is constant, but each worker’s productivity varies. Initially, when we hire more workers, they become more productive, perhaps because they have less ‘down time’ in switching between tasks. This means that the labour costs per snowboard must decline. At some point, however, the law of diminishing returns sets in: as before, each additional worker is paid a constant amount, but, as productivity declines the labour cost per snowboard increases.
The relationship between average labour productivity and average variable cost can be stated more precisely: Using W to define the wage, and L the amount of labour employed, the AVC can be written as follows:
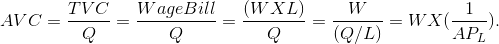
Writing the relationship in this way enables us to see the key role played by the productivity of workers in determining the shape of the AVC curve: When the denominator (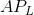 ) rises relative to the constant numerator (W), then the AVC must fall, and vice versa.
This is exactly what happens when production expands. Initially, average productivity increases relative to the fixed wage rate W, and therefore the AVC initially falls. At higher output
levels, the average productivity falls relative to the wage, and therefore AVC increases.
) rises relative to the constant numerator (W), then the AVC must fall, and vice versa.
This is exactly what happens when production expands. Initially, average productivity increases relative to the fixed wage rate W, and therefore the AVC initially falls. At higher output
levels, the average productivity falls relative to the wage, and therefore AVC increases.
In this numerical example the AP is at a maximum when six units of labour are employed and output is 175, and this is also the point where the AVC is at a minimum. This maximum/minimum relationship is also illustrated in Figure 8.2 and Figure 8.4.
The sum of fixed cost per unit of output and variable cost per unit of output yields total cost per unit of output, or average total cost. Typically, fixed costs are the dominant component of total costs at low output levels, but become less dominant at higher output levels. Unlike average variable costs, note that average fixed must decline with output. Thus, when the ATC curve eventually increases, it is because the increasing variable cost component eventually dominates the declining AFC component. In our example, this occurs when output increases from of 220 units (8 workers) to 235 (9 workers).
The marginal cost (MC) defines the cost of producing one more unit of output. In Table 8.2, the marginal cost of output is given in the final column. It is the additional cost of production divided by the additional number of units produced. For example, in going from 15 units of output to 40, total costs increase from $4000 to $5000. The MC is therefore $1000/25 = $40. We could also calculate the MC as the addition to variable costs rather than the addition to total costs, because the addition to each is the same—fixed costs are fixed. Hence:
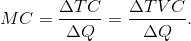
 Marginal cost of production is the cost of
producing each additional unit of output.
Marginal cost of production is the cost of
producing each additional unit of output.
Just as the behaviour of the AVC curve is determined by the AP curve, so too the behaviour of the MC is determined by the MP curve. When the MP of an additional worker exceeds the MP of the previous worker, this implies that the cost of the additional output produced by the last worker hired must be declining. The change in total cost of production that is associated with one more worker (DL) is the cost of that worker—his wage; and the change in output that this additional worker produces, DQ, is his marginal product. Therefore:
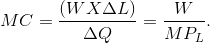
Consequently, with a constant wage, when the 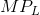 of workers
increases, the MC of output must decline, and vice versa; That is, the MC curve falls whenever the MP curve rises, and rises when the MP falls.
of workers
increases, the MC of output must decline, and vice versa; That is, the MC curve falls whenever the MP curve rises, and rises when the MP falls.
In our example, the 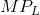 reaches a maximum when the fourth unit of
labour is employed (or 110 units of output are produced), and this also is where the MC is at a minimum. It follows that the marginal cost reaches a minimum at the output level where the MP
reaches a maximum.
reaches a maximum when the fourth unit of
labour is employed (or 110 units of output are produced), and this also is where the MC is at a minimum. It follows that the marginal cost reaches a minimum at the output level where the MP
reaches a maximum.
Finally, observe the interrelationship between the MC curve on the one hand and the ATC and AVC on the other. Note from Figure 8.4 that the MC cuts the AVC and the ATC at the minimum point of each of the latter. The logic behind this pattern is analogous to the logic of the relationship between marginal and average product curves: When the cost of an additional unit of output is less than the average, this reduces the average cost; whereas, if the cost of an additional unit of output is above the average, this raises the average cost. This must hold true regardless of whether we relate the MC to the ATC or the AVC.
Notation: throughout this text we use two abbreviations for average total cost: ATC and AC denote average total cost. The term ‘average cost’ is understood in economics to include both fixed and variable costs.
- 瀏覽次數:3172






