The elasticity decreases in going from high prices to low prices. This is true for most non-linear demand curves also. Two exceptions are when the demand curve is horizontal and when it is vertical.
When the demand curve is vertical, no quantity change results from a change in price from 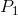 to
to 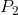 ,
as illustrated in Figure
4.2. Therefore, the numerator in Equation 4.1 is zero, and the elasticity has a zero value.
,
as illustrated in Figure
4.2. Therefore, the numerator in Equation 4.1 is zero, and the elasticity has a zero value.
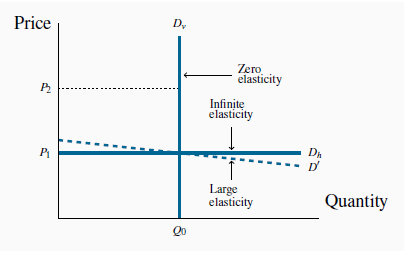
When the demand curve is vertical (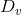 ), the elasticity is zero: a
change in price from
), the elasticity is zero: a
change in price from 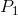 to
to 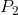 has no impact on the quantity demanded because the numerator in the elasticity formula
has a zero value. When D becomes more horizontal the elasticity becomes larger and larger at Qo, eventually becoming infinite.
has no impact on the quantity demanded because the numerator in the elasticity formula
has a zero value. When D becomes more horizontal the elasticity becomes larger and larger at Qo, eventually becoming infinite.
In the horizontal case, we say that the elasticity is infinite, which means that any percentage price change brings forth an infinite quantity change! This case is also illustrated in Figure 4.2 using the demand curve
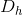 . As with the vertical demand curve, this is not immediately
obvious. So consider a demand curve that is almost horizontal, such as D' instead of
. As with the vertical demand curve, this is not immediately
obvious. So consider a demand curve that is almost horizontal, such as D' instead of 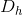 . In this instance, we can achieve large changes in quantity demanded by implementing very small price changes. In terms of
Equation 4.1, the numerator is large and the denominator small, giving rise to a large elasticity. Now imagine that this demand curve becomes ever more elastic (horizontal). The same quantity
response can be obtained with a smaller price change, and hence the elasticity is larger. Pursuing this idea, we can say that, as the demand curve becomes ever more elastic, the elasticity
value tends towards infinity.
. In this instance, we can achieve large changes in quantity demanded by implementing very small price changes. In terms of
Equation 4.1, the numerator is large and the denominator small, giving rise to a large elasticity. Now imagine that this demand curve becomes ever more elastic (horizontal). The same quantity
response can be obtained with a smaller price change, and hence the elasticity is larger. Pursuing this idea, we can say that, as the demand curve becomes ever more elastic, the elasticity
value tends towards infinity.
- 瀏覽次數:2356






