- It is very useful, as we shall see presently, to decompose a price change, which moves the consumer along his demand curve, into two components—an income effect and a
substitution effect. Figure
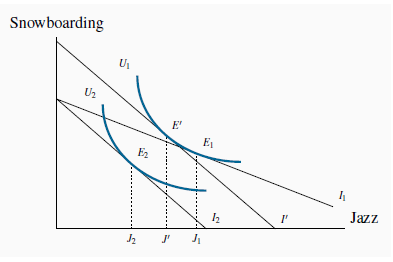
6.11 illustrates the impact of an increase in the price of jazz: The equilibrium moves from
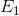 to
to 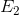 as a result of the budget constraint’s changing from
as a result of the budget constraint’s changing from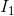 to
to 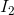 . This price increase reduces the demand for jazz in two ways. First, jazz becomes relatively more expensive compared with other goods, and this is reflected in the steeper price line.
Second, the price increase reduces the real purchasing power of the consumer’s income.
. This price increase reduces the demand for jazz in two ways. First, jazz becomes relatively more expensive compared with other goods, and this is reflected in the steeper price line.
Second, the price increase reduces the real purchasing power of the consumer’s income.
The equilibrium 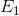 is disturbed by an increase in Pj that
rotates
is disturbed by an increase in Pj that
rotates 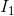 to
to 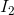 . The new equilibrium is
. The new equilibrium is 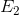 . The substitution effect is from
. The substitution effect is from 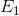 to E' – to a point on the initial indifference curve where the slope is the same as the slope of
to E' – to a point on the initial indifference curve where the slope is the same as the slope of 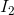 . From E' to
. From E' to 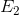 is the income effect; it is equivalent to a parallel shift in the budget constraint I' to
is the income effect; it is equivalent to a parallel shift in the budget constraint I' to 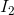 .
.
Consider an experiment in which we could give the consumer just enough income, at the new price, to attain the same level of utility as was originally attained, 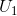 . The budget line that permits this is parallel to the constraint
. The budget line that permits this is parallel to the constraint 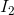 —the post price-change line—and tangent to U'. Call this imaginary budget line I', and let
it result in a tangency at E'. The reduction in jazz that is due solely to the change in the relative prices, and that could keep the consumer at the indifference level
—the post price-change line—and tangent to U'. Call this imaginary budget line I', and let
it result in a tangency at E'. The reduction in jazz that is due solely to the change in the relative prices, and that could keep the consumer at the indifference level 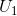 , is called the substitution effect of the price change. This is defined in the figure as
the distance from
, is called the substitution effect of the price change. This is defined in the figure as
the distance from 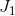 to
to 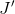 .
.
 The substitution effect of a price change is the
response of demand to a relative price change that maintains the consumer on the initial indifference curve.
The substitution effect of a price change is the
response of demand to a relative price change that maintains the consumer on the initial indifference curve.
The remaining impact of the price change on the demand for jazz—the move from 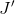 to
to 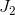 —is the income effect. The reason is that this move is associated with a parallel inward shift of the budget constraint. It is
therefore an income effect.
—is the income effect. The reason is that this move is associated with a parallel inward shift of the budget constraint. It is
therefore an income effect.
 The income effect of a price change is the
response of demand to the change in real income that moves the individual from the initial level to a new level of utility.
The income effect of a price change is the
response of demand to the change in real income that moves the individual from the initial level to a new level of utility.
Income and substitution effects are frequently thought of as being obscure. But this is not so. They are also very useful in understanding policy issues, such as subsidies and taxation. Let us turn to an application.
- 瀏覽次數:2406






