In Figure
5.5, the supply curve S represents the cost to the supplier, whereas 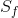 (the full cost) reflects, in addition, the cost of bad air to the population. Of course, we are assuming that this external cost
is ascertainable, in order to be able to characterize
(the full cost) reflects, in addition, the cost of bad air to the population. Of course, we are assuming that this external cost
is ascertainable, in order to be able to characterize 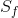 accurately. Note also that this illustration assumes that, as power output increases, the external cost per unit rises, because the difference between the two supply curves increases with
output. This implies that low levels of pollution do less damage: Perhaps the population has a natural tolerance for low levels, but higher levels cannot be tolerated easily and so the cost is
greater.
accurately. Note also that this illustration assumes that, as power output increases, the external cost per unit rises, because the difference between the two supply curves increases with
output. This implies that low levels of pollution do less damage: Perhaps the population has a natural tolerance for low levels, but higher levels cannot be tolerated easily and so the cost is
greater.
Despite the externality, an efficient level of production can still be defined. It is given by Q*, not 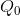 . To see why, consider the impact of reducing output by one unit from Q0. At Q0 the willingness of buyers to pay for the marginal
unit supplied is
. To see why, consider the impact of reducing output by one unit from Q0. At Q0 the willingness of buyers to pay for the marginal
unit supplied is 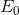 . The (private) supply cost is also
. The (private) supply cost is also 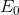 . But from a societal standpoint there is a pollution/health cost of
. But from a societal standpoint there is a pollution/health cost of
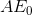 associated with that unit of production. The full cost, as
represented by
associated with that unit of production. The full cost, as
represented by 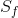 , exceeds the buyer’s valuation. Accordingly,
if the last unit of output produced is cut, society gains by the amount
, exceeds the buyer’s valuation. Accordingly,
if the last unit of output produced is cut, society gains by the amount 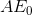 , because the cut in output reduces the excess of true cost over value.
, because the cut in output reduces the excess of true cost over value.
Applying this logic to each unit of output between 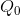 and Q*, it
is evident that society can increase its well-being by the dollar amount equal to the area E*
and Q*, it
is evident that society can increase its well-being by the dollar amount equal to the area E*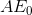 , as a result of reducing production.
, as a result of reducing production.
Next, consider the consequences of reducing output further from Q*. Note that pollution is being created here, and environmentalists frequently advocate that pollution should be reduced to zero. However, an efficient outcome may not involve a zero level of pollution! If the production of power were reduced below Q*, the loss in value to buyers, as a result of not being able to purchase the good, would exceed the full cost of its production.
If the government decreed that, instead of producing Q*, no pollution would be tolerated, then society would forgo the possibility of earning the total real surplus equal to the area UE*K. Economists do not advocate such a zero-pollution policy; rather, we advocate a policy that permits a “tolerable” pollution level – one that still results in net benefits to society. In this particular example, the total cost of the tolerated pollution equals the area between the private and full supply functions, KE*VR.
As a matter of policy, how is this market influenced to produce the amount Q* rather than 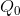 ? One option would be for the government to intervene directly with production quotas for each firm. An alternative would be to
impose a corrective tax on the good whose production causes the externality: With an appropriate increase in the price, consumers will demand a reduced quantity. In Figure 5.5 a tax equal to the
dollar value VE* would shift the supply curve upward by that amount and result in the quantity Q* being traded.
? One option would be for the government to intervene directly with production quotas for each firm. An alternative would be to
impose a corrective tax on the good whose production causes the externality: With an appropriate increase in the price, consumers will demand a reduced quantity. In Figure 5.5 a tax equal to the
dollar value VE* would shift the supply curve upward by that amount and result in the quantity Q* being traded.
 A corrective tax seeks to direct the market
towards a more efficient output.
A corrective tax seeks to direct the market
towards a more efficient output.
We are now venturing into the field of environmental policy, and this is explored in the following section. The key conclusion of the foregoing analysis is that an efficient working of the market continues to have meaning in the presence of externalities. An efficient output level still maximizes economic surplus where surplus is correctly defined.
- 瀏覽次數:2853






