Some ideas in this proof are due to Jerome Keisler (see references, p.201).
On page 28, I computed the derivative of sin tto be cos tas follows:
dx= sin(t+ dt) −sin t ,
= sin tcos dt
+ cos tsin dt−sin t
= cos tdt+ ... .
We want to prove prove that the error “. . . ” introduced by the small- angle approximations really is of order 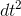 .
.
A quick and dirty way to check whether this is likely to be true is to use Inf to calculate sin(t+ dt) at some specific value of t. For example, at t= 1 we have this result:
: sin(1+d)
(0.84147)+(0.54030)d
+(-0.42074)d^2+(-0.09006)d^3
+(0.03506)d^4
The small-angle approximations give sin(1 + d) ≈sin 1 + (cos 1)d. The coefficients of the first two terms of the exact result are, as expected sin(1) = 0.84147 and cos(1) = 0.5403 ..., so although the small-angle approximations have introduced some errors, they involve only higher powers of dt, as claimed.
The demonstration with Inf has two shortcomings. One is that it only works for t= 1, but we need to prove that the result for all values of t. That doesn’t mean that the check for t= 1 was useless. Even though a general mathematical statement about all numbers can never be proved by demonstrating specific examples for which it succeeds, a single counterexample suffices to disproveit. The check for t= 1 was worth doing, because if the first term had come out to be 0.88888, it would have immediately disproved our claim, thereby saving us from wasting hours attempting to prove something that wasn’t true.
The other problem is that I’ve never explained how Inf calculates this kind of thing. The answer is that it uses something called a Taylor series, discussed in section 7.4. Using Inf here without knowing yet how Taylor series work is like using your calculator as a “black box” to extract the square root of √2 without knowing how it does it. Not knowing the inner workings of the black box makes the demonstration less than satisfying.
In any case, this preliminary check makes it sound like it’s reasonable to go on and try to produce a real proof. We have
sin(t+ dt) = sin t+ cos tdt−E ,
where the error Eintroduced by the approximations is
E= sin t(1 −cos dt)
+ cos t(dt−sin dt) .
Let the radius of the circle in figure a be one, so AD is cos dtand CD is sin dt. The area of the shaded pie slice is dt/2, and the area of triangle ABC is sin dt/2, so the error made in the approximation sin dt≈dtequals twice the area of the dish shape formed by line BC and arc BC. Therefore dt−sin dtis less than the area of rectangle CEBD. But CEBD has both an infinitesimal width and an infinitesimal height, so this error is of no more than order dt2 .
For the approximation cos dt≈1, the error (represented by BD) is
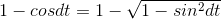 , which is less than
, which is less than 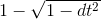 , since
, since
sin dt<dt. Therefore this error is of order 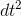 .
.
- 瀏覽次數:2726






