In the story of Gauss’s problem of adding up the numbers from 1 to100, one interpretation of the result, 5,050, is that the average of all the numbers from 1 to 100 is 50.5. This is the ordinary definition of an average: add up all the things you have, and divide by the number of things. (The result in this example makes sense, because half the numbers are from 1 to 50, and half are from 51 to 100, so the average is half-way between 50 and 51.)
Similarly, a definite integral can also be thought of as a kind of aver- age. In general, if 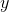 is a function of
is a function of 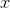 , then the average, or mean, value of
, then the average, or mean, value of 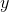 on the
interval from
on the
interval from 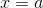 to
to 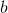 can be defined as
can be defined as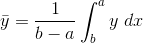
In the continuous case, dividing by b − a accomplishes the same
thing as dividing by the number of things in the discrete case.
Example
Show that the definition of the average makes sense in the case where the function is a constant.If 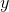 is a constant, then we can take it outside of the integral, so
is a constant, then we can take it outside of the integral, so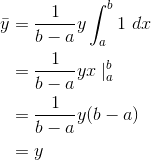
Example
Find the average value of the function 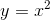 for values of
for values of 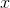 ranging from 0 to 1.
ranging from 0 to 1.
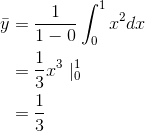
The mean value theorem
If the continuous function 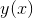 has the average value
has the average value 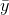 on the interval from
on the interval from 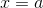 to
to 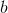 , then
, then 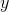 attains its average value at least once in that interval, i.e., there exists
attains its average value at least once in that interval, i.e., there exists 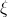 with
with 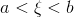 such that
such that 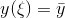 .
.
The mean value theorem is proved in Proof of the mean
value theorem. The special case in which 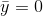 is known as
Rolle’s theorem.
is known as
Rolle’s theorem.
Example
Verify the mean value theorem for 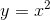 on the interval from 0 to 1.
on the interval from 0 to 1.
The mean value is 1/3, as shown in Example. This value is
achieved at 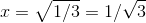 , which lies between 0 and 1.
, which lies between 0 and 1.
- 3187 reads






