In chapter 1, we saw that locating maxima and minima of functions may in general be fairly difficult, because there are so many different ways in which a function can attain an extremum: e.g., at an endpoint, at a place where its derivative is zero, or at a non-differentiable kink. The following theorem allows us to make a very general statement about all these possible cases, assuming only continuity.
The extreme value theorem states that if 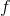 is a continuous
real-valued function on the real-number interval defined by
is a continuous
real-valued function on the real-number interval defined by 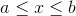 , then
, then 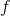 has maximum and minimum values on that interval, which are attained at specific points in the interval.
has maximum and minimum values on that interval, which are attained at specific points in the interval.
Let’s first see why the assumptions are necessary. If we weren’t confined to a finite interval, then 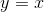 would be a counterexample, because it’s continuous and doesn’t have any maximum or minimum value. If we didn’t assume continuity,
then we could have a function defined as
would be a counterexample, because it’s continuous and doesn’t have any maximum or minimum value. If we didn’t assume continuity,
then we could have a function defined as 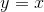 for
for 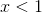 , and
, and 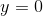 for
for 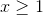 ; this function never gets bigger than 1, but it never attains a value of 1 for any specific value of
; this function never gets bigger than 1, but it never attains a value of 1 for any specific value of 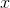 .
.
The extreme value theorem is proved, in a somewhat more general form,in Proof of the extreme value theorem.
Example
Find the maximum value of the polynomial 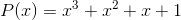 for
for
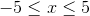 .
.
Polynomials are continuous, so the extreme value theorem guarantees that such a maximum exists. Suppose we try to find it by looking for a place where the derivative is zero. The derivative
is 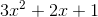 , and setting it equal to zero gives a quadratic
equation, but application of the quadratic formula shows that it has no real solutions. It appears that the function doesn’t have a maximum anywhere (even outside the interval of interest)
that looks like a smooth peak. Since it doesn’t have kinks or discontinuities, there is only one other type of maxi- mum it could have, which is a maxi- mum at one of its endpoints. Plugging
in the limits, we find
, and setting it equal to zero gives a quadratic
equation, but application of the quadratic formula shows that it has no real solutions. It appears that the function doesn’t have a maximum anywhere (even outside the interval of interest)
that looks like a smooth peak. Since it doesn’t have kinks or discontinuities, there is only one other type of maxi- mum it could have, which is a maxi- mum at one of its endpoints. Plugging
in the limits, we find 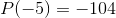 and
and 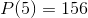 , so we conclude that the maximum value on this interval is 156.
, so we conclude that the maximum value on this interval is 156.
- 3989 reads






