When I first learned calculus, it seemed to me that if the derivative of 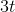 was 3, and the derivative of
was 3, and the derivative of 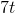 was 7, then the derivative of
was 7, then the derivative of 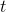 multiplied by
multiplied by 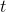 ought to be
just plain old
ought to be
just plain old 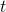 , not
, not 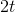 . The reason there's a factor of 2 in the correct answer is that
. The reason there's a factor of 2 in the correct answer is that 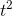 has two reasons to grow as
has two reasons to grow as 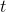 gets
bigger: it grows because the first factor of
gets
bigger: it grows because the first factor of 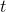 is increasing, but also because the second one is. In general, it's possible
to find the derivative of the product of two functions any time we know the derivatives of the individual functions.
is increasing, but also because the second one is. In general, it's possible
to find the derivative of the product of two functions any time we know the derivatives of the individual functions.
The product rule
If 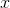 and
and 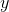 are both functions of
are both functions of 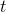 , then the derivative of their product is
, then the derivative of their product is 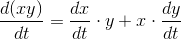
The proof is easy. Changing 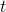 by an infinitesimal amount dt changes the product
by an infinitesimal amount dt changes the product 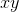 by an amount
by an amount
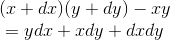
and dividing by dt makes this into
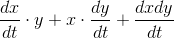
whose standard part is the result to be proved.
Example
Find the derivative of the function 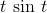 .
.
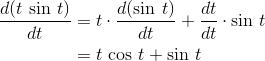
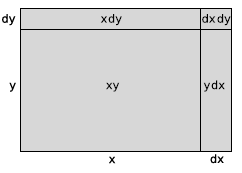
Figure 2.8 gives the
geometrical interpretation of the product rule. Imagine that the king, in his castle at the southwest corner of his rectangular kingdom, sends out a line of infantry to expand his territory to
the north, and a line of cavalry to take over more land to the east. In a time interval dt, the cavalry, which moves faster, covers a distance 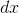 greater than that covered by the infantry,
greater than that covered by the infantry, 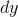 . However, the strip of territory conquered by the cavalry,
. However, the strip of territory conquered by the cavalry, 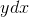 , isn't as great as it could have been, because in our example
, isn't as great as it could have been, because in our example 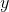 isn't as big as
isn't as big as 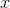 .
.
A helpful feature of the Leibniz notation is that one can easily use it to check whether the units of an answer make sense. If we measure distances in meters and time in seconds, then 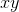 has units of square meters (area), and so does the change in the area,
has units of square meters (area), and so does the change in the area,
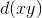 . Dividing by dt gives the number of square meters per second
being conquered. On the right-hand side of the product rule,
. Dividing by dt gives the number of square meters per second
being conquered. On the right-hand side of the product rule, 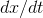 has
units of meters per second (velocity), and multiplying it by
has
units of meters per second (velocity), and multiplying it by 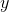 makes
the units square meters per second, which is consistent with the left-hand side. The units of the second term on the right likewise check out. Some beginners might be tempted to guess that the
product rule would be
makes
the units square meters per second, which is consistent with the left-hand side. The units of the second term on the right likewise check out. Some beginners might be tempted to guess that the
product rule would be 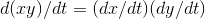 , but the Leibniz notation
instantly reveals that this can't be the case, because then the units on the left,
, but the Leibniz notation
instantly reveals that this can't be the case, because then the units on the left, 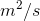 , wouldn't match the ones on the right,
, wouldn't match the ones on the right, 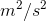 .
.
Because this unit-checking feature is so helpful, there is a special way of writing a second derivative in the Leibniz notation. What Newton called 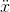 , Leibniz wrote as
, Leibniz wrote as
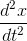
Although the different placement of the 2's on top and bottom seems strange and inconsistent to many beginners, it actually works out nicely. If 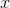 is a distance, measured in meters, and
is a distance, measured in meters, and 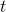 is a time, in units of seconds, then the second derivative is supposed to have units of
acceleration, in units of meters per second per second, also written
is a time, in units of seconds, then the second derivative is supposed to have units of
acceleration, in units of meters per second per second, also written 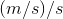 , or
, or 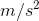 . (The acceleration of falling objects on Earth is
. (The acceleration of falling objects on Earth is 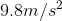 in these units.) The Leibniz notation is meant to suggest exactly this: the top of the fraction looks like it has units of
meters, because we're not squaring
in these units.) The Leibniz notation is meant to suggest exactly this: the top of the fraction looks like it has units of
meters, because we're not squaring 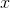 , while the bottom of the fraction looks like it has units of seconds squared,
because it looks like we're squaring dt. Therefore the units come out right. It's important to realize, however, that the symbol d isn't a number (not a real one, and not a hyperreal one,
either), so we can't really square it; the notation is not to be taken as a literal statement about infinitesimals.
, while the bottom of the fraction looks like it has units of seconds squared,
because it looks like we're squaring dt. Therefore the units come out right. It's important to realize, however, that the symbol d isn't a number (not a real one, and not a hyperreal one,
either), so we can't really square it; the notation is not to be taken as a literal statement about infinitesimals.
Example
A tricky use of the product rule is to find the derivative of 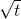 . Since
. Since 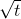 can be written as
can be written as 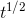 , we might suspect that the rule
, we might suspect that the rule 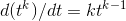 would work, giving a derivative
would work, giving a derivative 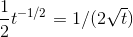 . However, the method from Rates of Change used to prove that rule proved in Derivatives of polynomials only work if
. However, the method from Rates of Change used to prove that rule proved in Derivatives of polynomials only work if 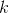 is an integer, so the best we could do would be to confirm our conjecture approximately by graphing or numerical
estimation.
is an integer, so the best we could do would be to confirm our conjecture approximately by graphing or numerical
estimation.
Using the product rule, we can write 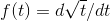 for our
unknown derivative, and back into the result using the product rule:
for our
unknown derivative, and back into the result using the product rule:
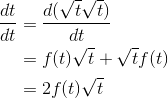
But 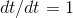 , so
, so 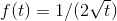 as claimed.
as claimed.
The trick used in Example can also be used to prove
that the power rule 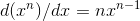 applies to cases where
applies to cases where 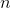 is an integer less than 0, but I'll instead prove this in Example by a technique that doesn't depend on a trick, and also
applies to values of
is an integer less than 0, but I'll instead prove this in Example by a technique that doesn't depend on a trick, and also
applies to values of 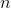 that aren't integers.
that aren't integers.
- 3423 reads






