You are here

Home » Brief Calculus » Techniques » Methods of integration Change of variable » Partial fractions

Complications

10 November, 2015 - 14:47
Available under Creative Commons-ShareAlike 4.0 International License.

There are two possible complications:

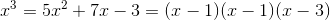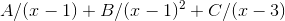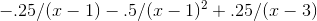First, the same factor may occur more than once, as in x^3=5x^2+7x-3=(x-1)(x-1)(x-3). In this example, we have to look for an answer of the form A/(x-1)+B/(x-1)^2+C/(x-3), the solution being -.25/(x-1)-.5/(x-1)^2+.25/(x-3).

Second, the roots may be complex. This is no show-stopper if you’re using computer software that handles complex numbers gracefully. (You can choose a c that makes the result real.) In fact, as discussed in Partial fractions revisited, some beautiful things can happen with complex roots. But as an alternative, any polynomial with real coefficients can be factored into linear and quadratic factors with real coefficients. 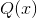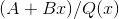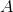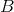For each quadratic factor Q(x), we then have a partial fraction of the form (A+Bx)/Q(x), where A and B can be determined by algebra. In Yacas, this can be done using the \texttt{Apart} function.

Example

Evaluate the integral

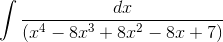
\int \frac{dx}{(x^4-8x^3+8x^2-8x+7)}

using the method of partial fractions. 　 

FindRealRoots(x^4-8*x^3
+8*x^2-8*x+7)
{f1.,7.}

Apart(1/(x^4-8*x^3
 +8*x^2-8*x+7))
 ((2*x)/25+3/50)/(x^2+1)
 +1/(300*(x-7))
 +(-1)/(12*(x-1))

We can now rewrite the integral like this:

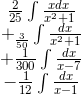
\begin{matrix} \frac{2}{25}\int \frac{xdx}{x^2+1} \\+_\frac{3}{50}\int \frac{dx}{x^2+1} \\ +\frac{1}{300}\int \frac{dx}{x-7} \\-\frac{1}{12}\int \frac{dx}{x-1} \end{matrix}

which we can evaluate as follows:

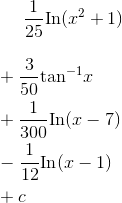
\frac{1}{25}\textrm{In}(x^2+1)\\ \begin{align*} &+\frac{3}{50}\textrm{tan}^{-1}x \\ &+ \frac{1}{300} \textrm{In}(x-7) \\ &-\frac{1}{12} \textrm{In} (x-1) \\ &+c \end{align*}

In fact, Yacas should be able to do the whole integral for us from scratch, but it’s best to understand how these things work under the hood, and to avoid being completely dependent on one particular piece of software. As an illustration of this gem of wisdom, I found that when I tried to make Yacas evaluate the integral in one gulp, it choked because the calculation became too complicated! Because I understood the ideas behind the procedure, I was still able to get a result through a mixture of computer calculations and working it by hand. Some- one who didn’t have the knowledge of the technique might have tried the integral using the software, seen it fail, and concluded, incorrectly, that the integral was one that simply couldn’t be done. A computer is no substitute for understanding.

  • 1589 reads