Is the transfer principle true?

The preceding section stated the transfer principle in rigorous language. But why should we believe that it’s true?

One approach would be to begin deducing things about the hyperreals, and see if we can deduce a contradiction. As a starting point, we can use the axioms of elementary algebra, because the transfer principle tells us that those apply to the hyperreals as well. Since we also assume that the Archimedean principle does nothold for the hyperreals, we can also base our reasoning on that, and therefore many of the things we can prove will be things that are true for the hyperreals, but false for the reals. This is essentially what mathematicians started doing immediately after Newton and Leibniz invented the calculus, and they were immediately successful in producing contradictions. However, they weren’t using formally defined logical systems, and they hadn’t stated anything as specific and rigorous as the transfer principle. In particular, they didn’t understand the need for anything like our restriction of the transfer principle to first-order logic. If we could reach a contradiction based on the more modern, rigorous statement of the transfer principle, that would be a different matter. It would tell us that one of two things was true: either (1) the hyperreal number system lacks logical self- consistency, or (2) both the hyperreals and the reals lack self-consistency.

Abraham Robinson proved, however, around 1960 that the reals and the hyperreals have the same level of consistency: one is self-consistent if and only if the other is. In other words, if the hyperreals harbor a ticking logical time bomb, so do the reals. Since most mathematicians don’t lose much sleep worrying about a lack of self-consistency in the real number system, this is generally taken as meaning that infinitesimals have been rehabilitated. In fact, it gives them an even higher level of respectability than they had in the era of Gauss and Euler, when they were widely used, but mathematicians knew a valid style of proof involving infinitesimals only because they’d slowly developed the right “Spidey sense.”

But how in the world could Robinson have proved such a thing? It seems like a daunting task. There is an infinite number of possible logical trains of argument in mathematics. How could he have demonstrated, with a stroke of a pen, that noneof them could ever lead to a contradiction (unless it indicated a contradiction lurking in the real number system as well)? Obviously it’s not possible to check them all explicitly.

The way modern logicians prove such things is usually by using models. For an easy example of a model, consider Euclidean geometry. Euclid believed that the following four postulates  1 were all self-evident:

These postulates, which today we would call “axioms,” played the same role with respect to Euclidean geometry that the elementary axioms of arithmetic play for the real number system.

Euclid also found that he needed a fifth postulate in order to prove many of his most important theorems, such as the Pythagorean theorem. I’ll state a different axiom that turns out to be equivalent to it:

5. Playfair’s version of the parallel postulate: Given any infinite line L, and any point P not on that line, there exists a unique infinite line through P that never crosses L.

The ancients believed this to be less obviously self-evident than the first four, partly because if you were given the two lines, it could theoretically take an infinite amount of time to inspect them and verify that they never crossed, even at some very distant point. Euclid avoided even mentioning infinite lines in postulates 1-4, and he considered postulate 5 to be so much less intuitively appealing in comparison that he organized the Elements so that the first 28 propositions were those that could be proved without resorting to it. Continuing the analogy with the reals and hyperreals, the parallel postulate plays the role of the Archimedean principle: a statement about infinity that we don’t feel quite so sure about.

For centuries, geometers tried to prove the parallel postulate from the first five. The trouble with this kind of thing was that it could be difficult to tell what was a valid proof and what wasn’t. The postulates were written in an ambiguous human language, not a formal logical system. As an example of the kind of confusion that could result, suppose we assume the following postulate, 5', in place of 5:

5': Given any infinite line L, and any point P not on that line, every infinite line through P crosses L.

Postulate 5'plays the role for noneuclidean geometry that the negation of the Archimedean principle plays for the hyperreals. It tells us we’re not in Kansas anymore. If a geometer can start from postulates 1-4 and 5'and arrive at a contradiction, then he’s made significant progress toward proving that postulate 5 has to be true based on postulates 1-4. (He would also have to disprove another version of the postulate, in which there is more than one parallel through P.) For centuries, there have been reasonable-sounding arguments that seemed to give such a contradiction. For instance, it was proved that a geometry with 5'in it was one in which distances were limited to some finite maximum. This would appear to contradict postulate 3, since there would be a limit on the radius of a circle. But there’s plenty of room for disagreement here, because the ancient Greeks didn’t have any notion of a set of real numbers. For them, the thing we would call a number was simply a finite straight line (line segment) with a certain length. If postulate 3 says that we can make a circle given any radius, it’s reasonable to interpret that as a statement that given any finite straightlineas the specification of the radius, we can make the circle. There is then no contradiction, because the too-long radius can’t be specified in the first place. This muddle is similar to the kind of confusion that reigned for centuries after Newton: did infinitesimals lead to contradictions?

In the 19th century, Lobachevsky and Bolyai came up with a version of Euclid’s axioms that was more rigorously defined, and that was care- fully engineered to avoid the kinds of contradictions that had previously been discovered in noneuclidean geometry. This is analogous to the in- vention of the transfer principle and the realization that the restriction to first-order logic was necessary. Lobachevsky and Bolyai slaved away for year after year proving new results in noneuclidean geometry, won- dering whether they would ever reach a contradiction. Eventually they started to doubt that there were ever going to be contradictions, and finally they proved that the contradictions didn’t exist.

The technique for proving consistency was to make a modelof the noneuclidean system. Consider geometry done on the surface of a sphere. The word “line” in the axioms now has to be understood as referring to a great circle, i.e., one with the same radius as the sphere. The parallel postulate fails, because parallels don’t exist: every great circle intersects every other great circle. One modification has to be made to the model in order to make it consistent with the first postulate. The constructions described in Euclid’s postulates are tacitly assumed to be unique (and in more rigorous formulations are explicitly stated to be so). We want there to be a unique line defined by any two distinct points. This works fine on the sphere as long as the points aren’t too far apart, but it fails if the points are antipodes, i.e., they lie at opposite sides of the sphere. For example, every line of longitude on the Earth’s surface passes through both poles. The solution to this problem is to modify what we mean by “point.” Points at each other’s antipodes are considered to be the same point. (Or, equivalently, we can do geometry on a hemisphere, but agree that when we go off one edge, we “wrap around” to the opposite side.)

This spherical model obeys all the postulates of this particular system of noneuclidean geometry. But consider now that we constructed it inside a surrounding three-dimensional space in which the parallel postulate does hold. Now suppose we keep on proving theorems in this system of noneuclidean geometry, filling up page after page with proofs using words like “line,” which we mentally associate with great circles on a certain sphere — and eventually we reach a contradiction. But now we can go back through our proofs, and in every place where the word “line” occurs we can cross it out with a red pencil and put in “great circle on this particular sphere.” It would now be a proof about Euclideangeometry, and the contradiction would prove that Euclideangeometry lacked self-consistency. We therefore arrive at the result that if noneuclidean geometry is inconsistent, so is Euclidean geometry. Since nobody believes that Euclidean geometry is inconsistent, this is considered the moral equivalent of proving noneuclidean geometry to be consistent.

If you’ve been keeping the system of analogies in mind as you read this story, it should be clear what’s coming next. If we want to prove that the hyperreals have the same consistency as the reals, we just have to construct a modelof the hyperreals using the reals. This is done in detail elsewhere (see Stroyan and Mathforum.org in the references, p. 201). I’ll just sketch the general idea. A hyperreal number is represented by an infinite sequence of real numbers. For example, the sequence

7, 7, 7, 7, ...

would be the hyperreal version of the number 7. A sequence like

1, 2, 3, ...

represents an infinite number, while

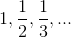
is infinitesimal. All the arithmetic operations are defined by applying them to the corresponding members of the sequences. For example, the sum of the 7, 7, 7, . . . sequence and the 1, 2, 3, . . . sequence would be 8, 9, 10, . . . , which we interpret as a somewhat larger infinite number.

The big problem in this approach is how to compare hyperreals, because a comparison like <is supposed to give an answer that is either true or false. It’s not supposed to give a hyperreal number as the result.

It’s clear that 8, 9, 10, . . . is greater than 1, 1, 1, . . . , because every member of the first sequence is greater than every member of the sec- ond one. But is 8, 9, 10, . . . greater than 9, 9, 9, . . . ? We want the answer to be “yes,” because we’re thinking of the first one as an infinite number and the second one as the ordinary finite number 9. The first sequence is indeed greater than the second at almost every one of the infinite number of places at which they could be compared. The only place where it loses the contest is at the very first position, and the only spot where we get a tie is the second one. Essentially the idea is that we want to define a concept of what happens “almost everywhere” on some infinite list. If one thing happens in an infinite number of places and something else only happens at some finite number of spots, then the definition of “almost everywhere” is clear. What’s harder is a comparison of something like these two sequences:

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, ...

and

1, 3, 1, 1, 3, 1, 1, 1, 3, 1, 1, 1, 1, 3, ...

where the second sequence has longer and longer runs of ones interspersed between the threes. The two sequences are never equal at any position, so clearly they can’t be considered to be equal as hyperreal numbers. But there is an infinite number of spots in which the first sequence is greater than the second, and likewise an infinite number in which it’s less. It seems as though there are more in which it’s greater, so we probably want to define the second sequence as being a hyperreal number that’s less than 2. The problem is that it can be very difficult to write down an acceptable definition of this “almost everywhere” notion. The answer is very technical, and I won’t go into it here, but it can be done. Because two sequences could be equal almost everywhere, we end up having to define a hyperreal number not as a particular sequence but as a set of sequences that are equal to each other almost everywhere.

With the construction of this model, it is possible to prove that the hyperreals have the same level of consistency as the reals.