In cylindrical coordinates (R, φ, z), zmeasures distance along the axis, Rmeasures distance from the axis, and φ is an angle that wraps around the axis.
The differential of volume in cylindrical coordinates can be written as dv = RdRdzdφ. This follows from adding a third dimension, along the zaxis, to the rectangle in figure d.
Example 100
Show that the expression for dvhas the right units.
Angles are unitless, since the definition of radian measure involves a distance divided by a distance. Therefore the only factors in the expression that have units are R, dR, and dz. If these three factors are measured, say, in meters, then their product has units of cubic meters, which is correct for a volume.
Example 101
Find the volume of a cone whose height is hand whose base has radius b.
Let’s plan on putting the zintegral on the outside of the sandwich. That means we need to express the radius rmax of the cone in terms of z. This
comes out nice and simple if we imagine the cone upside down, with its tip at the origin. Then since we have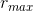 
(z= 0) = 0, and 
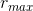(h) = b, evidently 
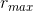= zb/h.
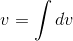
As a check, we note that the answer has units of volume. This is the classical result, known by the ancient Egyptians, that a cone has one third the volume of its enclosing cylinder.
In spherical coordinates (r, θ, φ), the coordinate rmeasures the distance from the origin, and θand φ are analogous to latitude and longitude, except that θis measured down from the pole rather than from the equator.
The differential of volume in spherical coordinates is dv =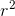 
sin θdrdθdφ.
Example 102
Find the volume of a sphere.
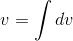
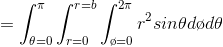
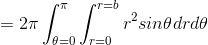
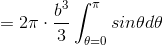
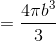
- 2172 reads
