Available under Creative Commons-ShareAlike 4.0 International License.
It is straightforward to prove a variant of l'Hopital's rule that allows us to do limits at infinity. The general proof is left as an exercise (Problem 3.8). The result is that l'H^opital's rule is equally valid when the limit is at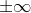 
rather than at some real number 
.
Example
Evaluate
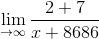
We could use a change of variable to make this into Example, which was solved using an ad hoc and multiple-step procedure. But having established the more general form of l’Hoˆ pital’s rule, we can do it in one step. Differentiation of the top and bot- tom produces
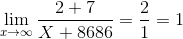
- 2142 reads
