It’s pretty trivial to generalize from e to b. If we write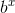 
as 
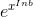, then we can substitute u = x ln b and reduce the b= e case to b =
e.
The generalization of the exponent of xfrom 2 to ais less straightforward. To do it with a= 2, we needed two integrations by parts, so clearly if we wanted to do a case with a= 37, we could do it with 37 integrations by parts. However, we would have no easy way to write down the complete answer without going through the whole tedious calculation. Furthermore, this is only going to work if ais a positive integer.
The obvious substitution is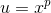 
, which leads to the form
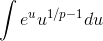. If the exponent 1/p−1
equals a nonnegative integer n, then through nintegrations by parts, we can reduce this to the form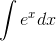 
. This requires p= 1, 1/2, 1/3, . . .
This is a mess if attacked by brute force. The trick is to reexpress the function using partial fractions:
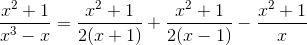
Writing u= x+ 1 and v= x−1, this becomes
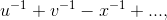
where . . . represents terms that will not survive multiple differentiations. Since du/dx= dv/dx= 1, the chain rule tells us that differentiation with respect to uor vis the same as differentiation with respect to x.
The result is 100!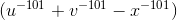
, where the notation 100!
means
1 ×2 ×...100.
- 瀏覽次數：1455
