The exponential function 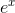 , where
, where 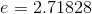 is the base of natural logarithms, comes constantly up in applications as diverse as
credit-card interest, the growth of animal populations, and electric circuits. For its derivative we have
is the base of natural logarithms, comes constantly up in applications as diverse as
credit-card interest, the growth of animal populations, and electric circuits. For its derivative we have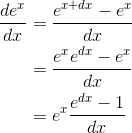
The second factor,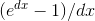 , doesn't have
, doesn't have 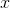 in it, so it must just be a constant. Therefore we know that the derivative of
in it, so it must just be a constant. Therefore we know that the derivative of 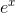 is simply
is simply 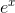 , multiplied
by some unknown constant,
, multiplied
by some unknown constant,
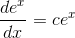
A rough check by graphing at, say 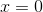 , shows that the slope is close to
1, so
, shows that the slope is close to
1, so  is close to 1. Numerical calculation also shows that, for
example,
is close to 1. Numerical calculation also shows that, for
example, 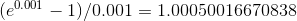 is very close to 1. But
how do we know it's exactly one when dx is really infinitesimal? We can use Inf:
is very close to 1. But
how do we know it's exactly one when dx is really infinitesimal? We can use Inf:
: [exp(d)-1]/d 1+0.5d+...
(The ... indicates where I've snipped some higher-order terms out of the output.) It seems clear that  is equal to 1 except for negligible terms involving higher powers of
is equal to 1 except for negligible terms involving higher powers of 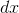 . A rigorous proof is given in Derivative of ex.
. A rigorous proof is given in Derivative of ex.
Example
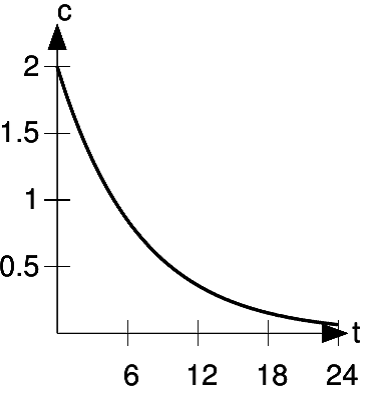
The concentration of a foreign substance in the bloodstream
generally falls off exponentially with time
as 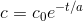 , where
, where 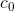 is the initial concentration, and a is a constant. For caffeine in
adults, a is typically about 7 hours. An example is shown in Figure 2.11. Differentiate the concentration with respect to time, and interpret the result. Check that the units of the result make
sense.
is the initial concentration, and a is a constant. For caffeine in
adults, a is typically about 7 hours. An example is shown in Figure 2.11. Differentiate the concentration with respect to time, and interpret the result. Check that the units of the result make
sense.
Using the chain rule,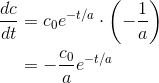 This can be interpreted as the rate at which caffeine Is being removed from
the blood and put into the person’s urine. It’s negative because the concentration is decreasing. According to the original expression for
This can be interpreted as the rate at which caffeine Is being removed from
the blood and put into the person’s urine. It’s negative because the concentration is decreasing. According to the original expression for 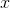 , a substance with a large a will take a long time to reduce its
concentration, since
, a substance with a large a will take a long time to reduce its
concentration, since 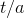 won’t be very big unless we have large
won’t be very big unless we have large 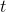 on top to compensate for the large
on top to compensate for the large  on the bottom. In other words, larger values of a represent substances
that the body has a harder time getting rid of efficiently. The derivative has a on the bottom, and the interpretation of this is that for a drug that is hard to eliminate, the rate at which
it is removed from the blood is low.
on the bottom. In other words, larger values of a represent substances
that the body has a harder time getting rid of efficiently. The derivative has a on the bottom, and the interpretation of this is that for a drug that is hard to eliminate, the rate at which
it is removed from the blood is low.
It makes sense that a has units of time, because the exponential
function has to have a unitless argument, so the units of 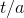 have to cancel out. The units of the result come from the factor
of
have to cancel out. The units of the result come from the factor
of 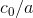 , and it makes sense that the units are concentration divided by time, because
the result represents the rate at which the concentration is changing.
, and it makes sense that the units are concentration divided by time, because
the result represents the rate at which the concentration is changing.
Example
Find the derivative of the function 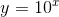 .
.
In general, one of the tricks to doing calculus is to rewrite functions in forms that you know how to handle. This one can be rewritten as a base-e exponent: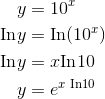
Applying the chain rule, we have the derivative of the exponential, which is just the same exponential, multiplied by the derivative of the inside stuff:
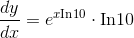 In other words, the “c” referred to in the discussion of the derivative of
In other words, the “c” referred to in the discussion of the derivative of 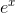 becomes
becomes 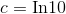 in the case of the base-10 exponential.
in the case of the base-10 exponential.
- 3823 reads






