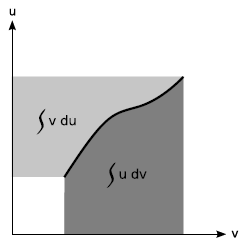
Figure 5.4 shows a technique called
integration by parts. If the integral 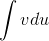 is easier than the
integral
is easier than the
integral 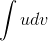 , then we can calculate the easier one, and then by
simple geometry determine the one we wanted. Identifying the large rectangle that surrounds both shaded areas, and the small white rectangle on the lower left, we have
, then we can calculate the easier one, and then by
simple geometry determine the one we wanted. Identifying the large rectangle that surrounds both shaded areas, and the small white rectangle on the lower left, we have
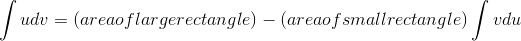
In the case of an indefinite integral, we have a similar relationship de- rived from the product rule:
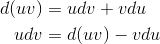
Integrating both sides, we have the following relation.
Integration by parts
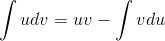
Since a definite integral can always be done by evaluating an indefinite integral at its upper and lower limits, one usually uses this form. Integrals don't usually come prepackaged in a form
that makes it obvious that you should use integration by parts. What the equation for integration by parts tells us is that if we can split up the integrand into two factors, one of which (the
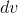 ) we know how to integrate, we have the option of changing the
integral into a new form in which that factor becomes its integral, and the other factor becomes its derivative. If we choose the right way of splitting up the integrand into parts, the result
can be a simplification.
) we know how to integrate, we have the option of changing the
integral into a new form in which that factor becomes its integral, and the other factor becomes its derivative. If we choose the right way of splitting up the integrand into parts, the result
can be a simplification.
Example
Evaluate
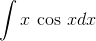
There are two obvious possibilities for splitting up the integrand into factors,
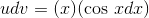 or
or
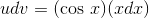
The first one is the one that lets us make progress. If 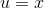 , then
, then
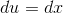 , and if
, and if 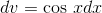 , then integration gives
, then integration gives 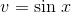 .
.
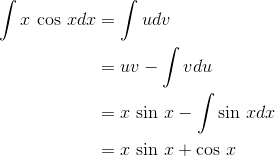
Of the two possibilities we considered for 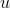 and
and 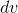 , the reason this one helped was that differentiating
, the reason this one helped was that differentiating 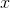 gave
gave 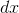 , which was simpler, and integrating
, which was simpler, and integrating 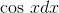 gave
gave 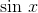 , which was no more complicated than before. The second possibility would have made things worse rather than better, because
integrating
, which was no more complicated than before. The second possibility would have made things worse rather than better, because
integrating 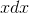 would have given
would have given 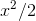 , which would have been more complicated rather than less.
, which would have been more complicated rather than less.
Example
Evaluate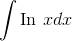
This one is a little tricky, because it isn’t explicitly written as a product, and yet we can attack it using integration by parts. Let 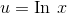 and
and 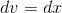
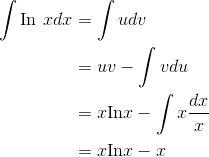
Example
Evaluate 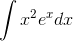
Integration by parts lets us split the integrand into two factors, integrate one, differentiate the other, and then do that integral. Integrating or differentiating 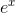 does nothing. Integrating
does nothing. Integrating 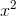 increases the exponent, which makes the problem look harder, whereas differentiating
increases the exponent, which makes the problem look harder, whereas differentiating 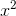 knocks the exponent down a step,
which makes it look easier. Let
knocks the exponent down a step,
which makes it look easier. Let 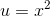 and
and 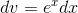 , so that
, so that 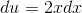 and
and 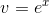 . We then have
. We then have
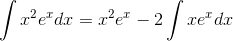 Although we don’t
immediately know how to evaluate this new integral, we can subject it to the same type of inte- gration by parts, now with
Although we don’t
immediately know how to evaluate this new integral, we can subject it to the same type of inte- gration by parts, now with 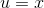 and
and 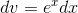 . After the second integra- tion by parts, we have:
. After the second integra- tion by parts, we have:
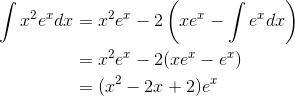
- 7808 reads






