Consider an example like this:
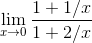
This is an indeterminate form like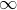 
/
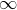rather than the 0/0 form for which we’ve already proved l’Hopital’s rule. As
proved in Proofs of the
generalizations of l’Hoˆ pital’s rule, l’Hopital’s rule applies to examples like this as well.
Example
Evaluate
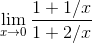Both the
numerator and the denominator go to infinity. Differentiation of the top and bottom gives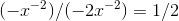 
. We can see that the reason the rule worked was that (1) the constant terms were irrelevant because they become negligible as
the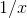 
terms blow up; and (2) differentiating the blowing-up
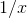terms makes them into the same
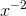on top and bottom, which cancel.
Note that we could also have gotten this result without l’Hopital’s rule, simply by multiplying both the top and the bottom of the original expression by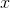 
in order to rewrite it as 
.
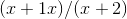- 1783 reads
