Available under Creative Commons-ShareAlike 4.0 International License.
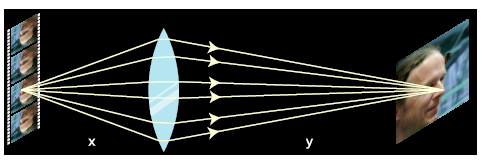
Figure 2.14
A set of light rays is emitted from the tip of the glamorous movie star’s nose on the film, and reunited to form a spot on the screen which is the image of the same point on his nose. The
distances have been distorted for clarity. The distance y represents the entire length of the theater from front to back.
In a movie theater, the image on the screen is formed by a lens in the projector, and originates from one of the frames on the strip of celluloid film (or, in the newer digital projection
systems, from a liquid crystal chip). Let the distance from the film to the lens be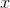 
, and let the distance from the lens to the screen be 
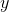. The projectionist needs to adjust 
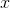so that it is properly matched with 
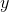, or else the image will be
out of focus. There is therefore a fixed relationship between 
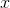and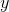 
, and this relationship is of the form
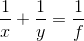
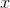, and let the distance from the lens to the screen be 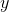. The projectionist needs to adjust 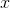so that it is properly matched with 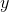, or else the image will be
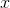out of focus. There is therefore a fixed relationship between and 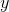, and this relationship is of the form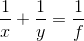
where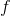 
is a property of the lens, called its focal length. A stronger lens has a shorter focal length. Since the theater is large, and
the projector is relatively small, 
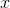is much less than 
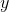. We can see from the equation that if 
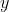is sufficiently
large, the left-hand side of the equation is dominated by the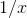 
term, and we have 
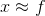. Since the 
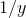term doesn't completely vanish, we must have 
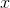slightly greater than 
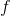, so that
the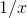 
term is slightly less than 
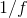. Let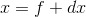 
, and approximate 
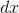as being infinitesimally small. Find a simple expression for 
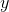in terms
of 
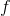and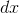 
.
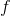is a property of the lens, called its focal length. A stronger lens has a shorter focal length. Since the theater is large, and
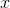the projector is relatively small, is much less than 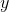. We can see from the equation that if 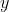is sufficiently
large, the left-hand side of the equation is dominated by the 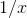term, and we have 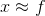. Since the 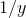term doesn't completely vanish, we must have 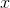slightly greater than 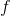, so that
the 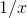term is slightly less than 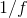. Let 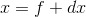, and approximate 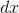as being infinitesimally small. Find a simple expression for 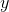in terms
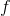of and .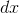
- 瀏覽次數：2799
