Sometimes an unfamiliar-looking integral can be made into a familiar one by substituting a new variable for an old one. For example, we know how to integrate 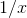 — the answer is
— the answer is 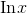 — but what about
— but what about
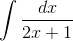
Let 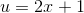 . Differentiating both sides, we have
. Differentiating both sides, we have 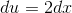 , or
, or 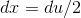 ,so
,so
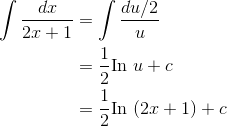
This technique is known as a change of variable or a substitution. (Because the letter u is of- ten employed, you may also see it called 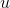 -substitution.)
-substitution.)
In the case of a definite integral, we have to remember to change the limits of integration to reflect the new variable.
Example
Evaluate 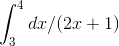 .
.
As before, let 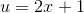 .
.
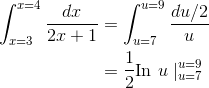
Here the notation 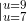 means to evaluate the function at
7 and 9, and sub- tract the former from the latter. The result is
means to evaluate the function at
7 and 9, and sub- tract the former from the latter. The result is
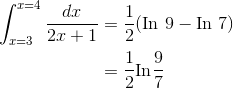
Sometimes, as in the next example, a clever substitution is the secret to doing a seemingly impossible integral.
Example
Evaluate
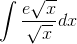
The only hope for reducing this to a form we can do is to let 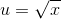 . Then
. Then 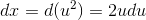 , so
, so
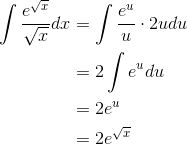
Example really isn't so tricky, since there was only one logical choice for the substitution that had any hope of working. The following is a little more dastardly.
Example
Evaluate
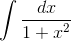
The substitution that works is 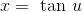 . First let’s see
what this does to the expression
. First let’s see
what this does to the expression 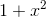 . The familiar identity
. The familiar identity
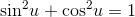
when divided by 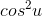 , gives
, gives
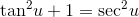
so 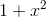 becomes
becomes 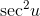 . But differentiating both sides of
. But differentiating both sides of 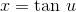 gives
gives
![\begin{align*} dx &=d[\textrm{sin } u(\textrm{cos }u)^{-1}] \\ &=(\textrm{dsin} u)(\textrm{cos }u)^{-1}+(\textrm{sin }u)d\left [ (\textrm{cos }u)^{-1} \right ] \\ &= (1+\textrm{tan}^2u)du\\ &= \textrm{sec}^2u du \end{align*}](/system/files/resource/33/33298/33658/media/eqn-img_27.gif)
so the integral becomes
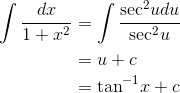
Integrate(x) 1/(1+x^2) ArcTan(x)
Another possible answer is that you can usually smell the possibility of this type of substitution, involving a trig function, when the thing to be integrated contains something reminiscent
of the Pythagorean theorem, as suggested by Figure 5.2. The 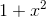 looks like what
you’d get if you had a right triangle with legs 1 and
looks like what
you’d get if you had a right triangle with legs 1 and 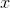 , and were
using the Pythagorean theorem to find its hypotenuse.
, and were
using the Pythagorean theorem to find its hypotenuse.
Example
Evaluate 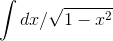
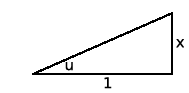
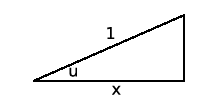
The 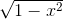 looks like what you’d get if you had a right
triangle with hypotenuse 1 and a leg of length
looks like what you’d get if you had a right
triangle with hypotenuse 1 and a leg of length 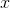 , and were using the
Pythagorean theorem to find the other leg, as in Figure 5.3. This motivates us to try the substitution
, and were using the
Pythagorean theorem to find the other leg, as in Figure 5.3. This motivates us to try the substitution 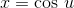 , which gives
, which gives 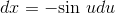 and
and  . The result is
. The result is
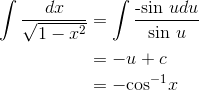
- 8305 reads






