The second-most important discrete-time signal is the unit sample, which is defined to be
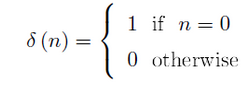
Unit Sample

Examination of a discrete-time signal's plot, like that of the cosine signal shown in Figure 2.7 (Discrete-Time Cosine Signal), reveals that all signals consist of a sequence of delayed and scaled unit samples. Because the value of a sequence at each integer m is denoted by s (m) and the unit sample delayed to occur at m is written δ (n − m), we can decompose any signal as a sum of unit samples delayed to the appropriate location and scaled by the signal value.
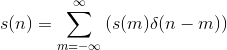
This kind of decomposition is unique to discrete-time signals, and will prove useful subsequently.
Discrete-time systems can act on discrete-time signals in ways similar to those found in analog signals and systems. Because of the role of software in discrete-time systems, many more different systems can be envisioned and "constructed" with programs than can be with analog signals. In fact, a special class of analog signals can be converted into discrete-time signals, processed with software, and converted back into an analog signal, all without the incursion of error. For such signals, systems can be easily produced in software, with equivalent analog realizations difficult, if not impossible, to design.
- 2857 reads






