Intuitive Way of Solving Op-Amp Circuits

Available under Creative Commons-ShareAlike 4.0 International License.

When we meet op-amp design specifications, we can simplify our circuit calculations greatly, so much so that we don't need the op-amp's circuit model to determine the transfer function. Here is our inverting amplifier.

Figure 3.45 op-amp

Figure 3.46 op-amp 2

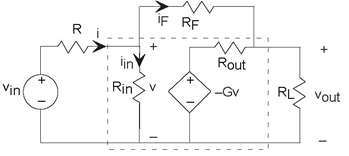
When we take advantage of the op-amp's characteristics large input impedance, large gain, and small output impedance we note the two following important facts.

The current i_in must be very small. The voltage produced by the dependent source is 10⁵ times the voltage v. Thus, the voltage v must be small, which means that 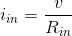$i_{in}=\frac{v}{R_{in}}$ in must be tiny. For example, if the output is about 1 V, the voltage v = 10⁻⁵V, making the current i_in = 10⁻¹¹ A. Consequently, we can ignore i_in in our calculations and assume it to be zero.
Because of this assumption essentially no current flow through R_in the voltage v must also be essentially zero. This means that in op-amp circuits, the voltage across the op-amp's input is basically zero.

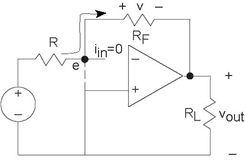
Armed with these approximations, let's return to our original circuit as shown in Figure 3.46. The node voltage e is essentially zero, meaning that it is essentially tied to the reference node. Thus, the current through the resistor R equals 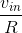$\frac{v_{in}}{R}$ . Furthermore, the feedback resistor appears in parallel with the load resistor. Because the current going into the op-amp is zero, all of the current flowing through R flows through the feedback resistor (iF = i)! 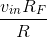The voltage across the feedback resistor v equals $\frac{v_{in}R_F}{R}$ . 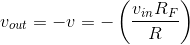Because the left end of the feedback resistor is essentially attached to the reference node, the voltage across it equals the negative of that across the output resistor: $v_{out}=-v=-\left ( \frac{v_{in}R_F}{R} \right )$ . Using this approach makes analyzing new op-amp circuits much easier. When using this technique, check to make sure the results you obtain are consistent with the assumptions of essentially zero current entering the op-amp and nearly zero voltage across the op-amp's inputs.

Example 3.8

Figure 3.47 Two Source Circuit

Two-source, single-output op-amp circuit example.

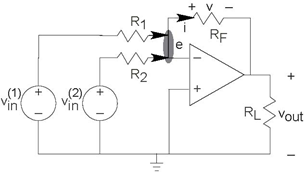
Let's try this analysis technique on a simple extension of the inverting amplifier confguration shown in Figure 3.47 (Two Source Circuit). If either of the source-resistor combinations were not present, the inverting amplifier remains, and we know that transfer function. By superposition, we know that the input-output relation is
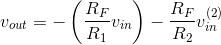
$v_{out}=-\left ( \frac{R_F}{R_1}v_{in} \right )-\frac{R_F}{R_2}v_{in}^{\left ( 2 \right )}$
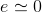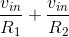When we start from scratch, the node joining the three resistors is at the same potential as the reference, $e\simeq 0$ , and the sum of currents flowing into that node is zero. Thus, the current i flowing in the resistor RF equals $\frac{v_{in}}{R_1}+\frac{v_{in}}{R_2}$ . Because the feedback resistor is essentially in parallel with the load resistor, the voltages must satisfy v = −v_out. In this way, we obtain the input-output relation given above.

What utility does this circuit have? Can the basic notion of the circuit be extended without bound?

瀏覽次數：5162

您在這裡

Intuitive Way of Solving Op-Amp Circuits