Sinusoids

Available under Creative Commons-ShareAlike 4.0 International License.

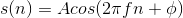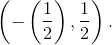Discrete-time sinusoids have the obvious form $s(n)=Acos(2\pi fn+\phi)$ . As opposed to analog complex exponentials and sinusoids that can have their frequencies be any real value, frequencies of their discrete time counterparts yield unique waveforms only when f lies in the interval $\left ( -\left ( \frac{1}{2} \right ),\frac{1}{2} \right ).$ . This property can be easily understood by noting that adding an integer to the

frequency of the discrete-time complex exponential has no effect on the signal's value.

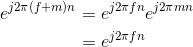
$\begin{align*} e^{j2\pi(f+m)n}&=e^{j2\pi fn}e^{j2\pi mn}\\ &=e^{j2\pi fn}\\ \end{align*}$

This derivation follows because the complex exponential evaluated at an integer multiple of 2π equals one.

瀏覽次數：1612

您在這裡

Sinusoids