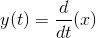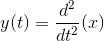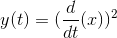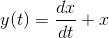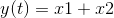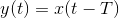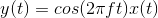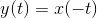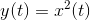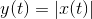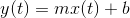Systems that don't change their input-output relation with time are said to be time-invariant. The mathematical way of stating this property is to use the signal delay concept described in Delay.
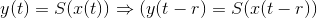
If you delay (or advance) the input, the output is similarly delayed (advanced). Thus, a time-invariant system responds to an input you may supply tomorrow the same way it responds to the same input applied today; today's output is merely delayed to occur tomorrow.
The collection of linear, time-invariant systems are the most thoroughly understood systems. Much of the signal processing and system theory discussed here concentrates on such systems. For example, electric circuits are, for the most part, linear and time-invariant. Nonlinear ones abound, but characterizing them so that you can predict their behavior for any input remains an unsolved problem.
|
Input-Output Relation |
Linear |
Time-Invariant |
|
|
yes |
yes |
|
|
yes |
yes |
|
|
no |
yes |
|
|
yes |
yes |
|
|
yes |
yes |
|
|
yes |
yes |
|
|
yes |
no |
|
|
yes |
no |
|
|
no |
yes |
|
|
no |
yes |
|
|
no |
yes |
- 瀏覽次數:4149