Solutions to Exercises in Chapter 5

Available under Creative Commons-ShareAlike 4.0 International License.

Solution to Exercise 5.2.1

For b-bit signed integers, the largest number is 2^b⁻¹ − 1. For b = 32, we have 2,147,483,647 and for b = 64, we have 9,223,372,036,854,775,807 or about 9.2 × 10¹⁸ .

Solution to Exercise 5.2.2

In floating point, the number of bits in the exponent determines the largest and smallest representable numbers. For 32-bit floating point, the largest (smallest) numbers are 2^±(127) =1.7 × 10³⁸ (5.9 × 10⁻³⁹). For 64-bit floating point, the largest number is about 10⁹⁸⁶³.

Solution to Exercise 5.2.3

25 = 11011₂ and 7 = 111₂. We find that 11001₂ + 111₂ = 100000₂ = 32.

Solution to Exercise 5.3.1

The only effect of pulse duration is to unequally weight the spectral repetitions. Because we are only concerned with the repetition centered about the origin, the pulse duration has no significant effect on recovering a signal from its samples.

Solution to Exercise 5.3.2

Figure 5.33

The square wave's spectrum is shown by the bolder set of lines centered about the origin. The dashed lines correspond to the frequencies about which the spectral repetitions (due to sampling with T_s = 1) occur. As the square wave's period decreases, the negative frequency lines move to the left and the positive frequency ones to the right.

Solution to Exercise 5.3.3

The simplest bandlimited signal is the sine wave. At the Nyquist frequency, exactly two samples/period would occur. Reducing the sampling rate would result in fewer samples/period, and these samples would appear to have arisen from a lower frequency sinusoid.

Solution to Exercise 5.4.1

The plotted temperatures were quantized to the nearest degree. Thus, the high temperature's amplitude was quantized as a form of A/D conversion.

Solution to Exercise 5.4.2

The signal-to-noise ratio does not depend on the signal amplitude. With an A/D range of [−A, A], the quantization interval 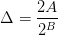$\Delta =\frac{2A}{2^{B}}$ and the signal's rms value (again assuming it is a sinusoid) is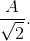 $\frac{A}{\sqrt{2}}.$

Solution to Exercise 5.4.3

Solving 2⁻^B = .001 results in B = 10 bits.

Solution to Exercise 5.4.4

A 16-bit A/D converter yields a SNR of 6 × 16 + 10log1.5 = 97.8 dB.

Solution to Exercise 5.6.1

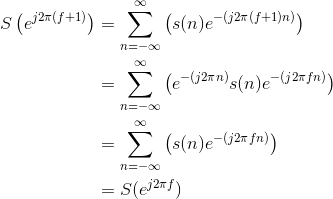
$\begin{align*} S\left ( e^{j2\pi (f+1)} \right ) &= \sum_{n=-\infty }^{\infty}\left ( s(n)e^{-\left ( j2\pi (f+1)n \right )} \right ) \\ &= \sum_{n=-\infty }^{\infty}\left ( e^{-(j2\pi n)}s(n)e^{-(j2\pi fn)} \right ) \\ &= \sum_{n=-\infty }^{\infty} \left ( s(n)e^{-(j2\pi fn)} \right ) \\ &= S(e^{j2\pi f}) \end{align*}$

(5.56)

Solution to Exercise 5.6.2

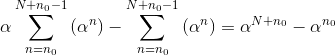
$\alpha \sum_{n=n_{0}}^{N+n_{0}-1}\left ( \alpha ^{n} \right )-\sum_{n=n_{0}}^{N+n_{0}-1}\left ( \alpha ^{n} \right ) = \alpha ^{N+n_{0}}-\alpha ^{n_{0}}$

which, after manipulation, yields the geometric sum formula.

Solution to Exercise 5.6.3

If the sampling frequency exceeds the Nyquist frequency, the spectrum of the samples equals the analog spectrum, but over the normalized analog frequency fT . Thus, the energy in the sampled signal equals the original signal's energy multiplied by T.

Solution to Exercise 5.7.1

This situation amounts to aliasing in the time-domain.

Solution to Exercise 5.8.1

When the signal is real-valued, we may only need half the spectral values, but the complexity remains unchanged. If the data are complex-valued, which demands retaining all frequency values, the complexity is again the same. When only K frequencies are needed, the complexity is O (KN).

Solution to Exercise 5.9.1

If a DFT required 1ms to compute, and signal having ten times the duration would require 100ms to compute. Using the FFT, a 1ms computing time would increase by a factor of about 10log₂10 = 33 , a factor of 3 less than the DFT would have needed.

Solution to Exercise 5.9.2

The upper panel has not used the FFT algorithm to compute the length-4 DFTs while the lower one has. The ordering is determined by the algorithm.

Solution to Exercise 5.9.3

The transform can have any greater than or equal to the actual duration of the signal. We simply "pad" the signal with zero-valued samples until a computationally advantageous signal length results. Recall that the FFT is an algorithm to compute the DFT (Section 5.7). Extending the length of the signal this way merely means we are sampling the frequency axis more fnely than required. To use the Cooley-Tukey algorithm, the length of the resulting zero-padded signal can be 512, 1024, etc. samples long.

Solution to Exercise 5.10.1

Number of samples equals 1.2 × 11025 = 13230. The datarate is 11025 × 16 = 176.4 kbps. The storage required would be 26460 bytes.

Solution to Exercise 5.10.2

The oscillations are due to the boxcar window's Fourier transform, which equals the sinc function.

Solution to Exercise 5.10.3

These numbers are powers-of-two, and the FFT algorithm can be exploited with these lengths. To compute a longer transform than the input signal's duration, we simply zero-pad the signal.

Solution to Exercise 5.11.1

In discrete-time signal processing, an amplifier amounts to a multiplication, a very easy operation to perform.

Solution to Exercise 5.12.1

The indices can be negative, and this condition is not allowed in MATLAB. To fix it, we must start the signals later in the array.

Solution to Exercise 5.12.2

Such terms would require the system to know what future input or output values would be before the current value was computed. Thus, such terms can cause difficulties.

Solution to Exercise 5.13.1

It now acts like a bandpass filter with a center frequency of f₀and a bandwidth equal to twice of the original lowpass filter.

Solution to Exercise 5.14.1

The DTFT of the unit sample equals a constant (equaling 1). Thus, the Fourier transform of the output equals the transfer function.

Solution to Exercise 5.14.2

In sampling a discrete-time signal's Fourier transform L times equally over [0, 2π) to form the DFT, the corresponding signal equals the periodic repetition of the original signal.

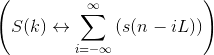
$\left ( S(k)\leftrightarrow \sum_{i=-\infty }^{\infty }\left ( s(n-iL) \right ) \right )$

(5.57)

To avoid aliasing (in the time domain), the transform length must equal or exceed the signal's duration.

Solution to Exercise 5.14.3

The difference equation for an FIR filter has the form

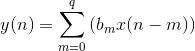
$y(n)=\sum_{m=0}^{q}\left ( b_{m}x(n-m) \right )$

(5.58)

The unit-sample response equals

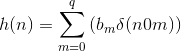
$h(n)=\sum_{m=0}^{q}\left ( b_{m}\delta (n0m) \right )$

(5.59)

which corresponds to the representation described in a problem (Discrete-Time Systems in the Time-Domain) of a length-q boxcar filter.

Solution to Exercise 5.14.4

The unit-sample response's duration is q +1 and the signal's N_x. Thus the statement is correct.

Solution to Exercise 5.15.1

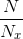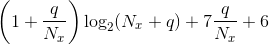Let N denote the input's total duration. The time-domain implementation requires a total of N(2q + 1) computations, or 2q +1 computations per input value. In the frequency domain, we split the input into $\frac{N}{N_{x}}$ sections, each of which requires $\left ( 1+\frac{q}{N_{x}} \right )\log_{2}(N_{x}+q)+7\frac{q}{N_{x}}+6$ per input in the section. Because we divide again by N_x to find the number of computations per input value in the entire input, this quantity decreases as N_x increases. For the time-domain implementation, it stays constant.

Solution to Exercise 5.15.2

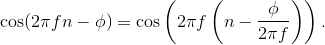
$\cos(2\pi fn-\phi )=\cos\left ( 2\pi f\left ( n-\frac{\phi }{2\pi f} \right ) \right ).$

The delay is not computational delay here the plot shows the first output value is aligned with the filter's first input although in real systems this is an important consideration. Rather, the delay is due to the filter's phase shift: A phase-shifted sinusoid is equivalent to a time-delayed one: 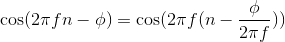$\cos(2\pi fn-\phi )=\cos(2\pi f(n-\frac{\phi }{2\pi f}))$ All filters have phase shifts. This delay could be removed if the filter introduced no phase shift. Such filters do not exist in analog form, but digital ones can be programmed, but not in real time. Doing so would require the output to emerge before the input arrives!

Solution to Exercise 5.16.1

We have p + q +1 multiplications and p + q − 1 additions. Thus, the total number of arithmetic operations equals 2(p + q).

瀏覽次數：5867

您在這裡

Solutions to Exercises in Chapter 5