Solution to Exercise 4.2.1
Because of Euler's relation,
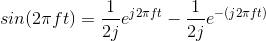
Thus, 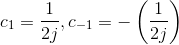 , and the other
coefficients are zero.
, and the other
coefficients are zero.
Solution to Exercise 4.2.2
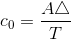 . This quantity clearly corresponds to the periodic pulse
signal's average value.
. This quantity clearly corresponds to the periodic pulse
signal's average value.
Solution to Exercise 4.3.1
Write the coefficients of the complex Fourier series in Cartesian form as ck = Ak + jBk and substitute into the expression for the complex Fourier series.
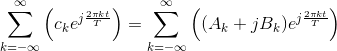
Simplifying each term in the sum using Euler’s formula.
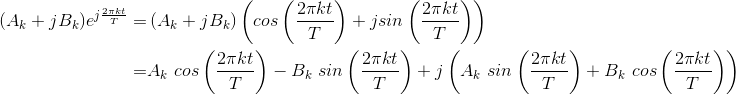
We now combine terms that have the same frequency index in magnitude. Because the signal is real-valued, the coefficients of the complex Fourier series have
conjugate symmetry: c−k = ck*or A−k = Ak and B−k = −Bk. After we add the positive-indexed and negative-indexed terms, each term in the Fourier series becomes
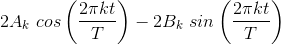 . To obtain the classic Fourier series (4.11), we must have 2Ak= akand 2Bk = −bk.
. To obtain the classic Fourier series (4.11), we must have 2Ak= akand 2Bk = −bk.
Solution to Exercise 4.3.2
The average of a set of numbers is the sum divided by the number of terms. Viewing signal integration as the limit of a Riemann sum, the integral corresponds to the average.
Solution to Exercise 4.3.3
We found that the complex Fourier series coefficients are given by 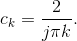 The coefficients are pure imaginary, which means ak
=0. The coefficients of the sine terms are given by bk = − (2Im (ck)) so that
The coefficients are pure imaginary, which means ak
=0. The coefficients of the sine terms are given by bk = − (2Im (ck)) so that
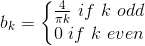
Thus, the Fourier series for the square wave is
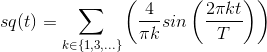
Solution to Exercise 4.4.1
The rms value of a sinusoid equals its amplitude divided by 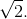 As a half-wave
rectified sine wave is zero during half of the period, its rms value is
As a half-wave
rectified sine wave is zero during half of the period, its rms value is 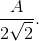 since the integral of the squared half-wave rectified sine wave equals half that of a squared sinusoid.
since the integral of the squared half-wave rectified sine wave equals half that of a squared sinusoid.
Solution to Exercise 4.4.2
Total harmonic distortion equals 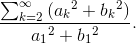 Clearly, this quantity is most easily computed in the frequency domain. However, the numerator equals the square of the signal's rms
value minus the power in the average and the power in the first harmonic.
Clearly, this quantity is most easily computed in the frequency domain. However, the numerator equals the square of the signal's rms
value minus the power in the average and the power in the first harmonic.
Solution to Exercise 4.5.1
Total harmonic distortion in the square wave is 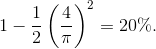
Solution to Exercise 4.6.1
N signals directly encoded require a bandwidth of 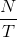 . Using a binary
representation, we need
. Using a binary
representation, we need 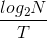 . For N =
128, the binary-encoding scheme has a factor of
. For N =
128, the binary-encoding scheme has a factor of 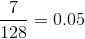 smaller bandwidth. Clearly, binary encoding is superior.
smaller bandwidth. Clearly, binary encoding is superior.
Solution to Exercise 4.6.2
We can use N different amplitude values at only one frequency to represent the various letters.
Solution to Exercise 4.7.1
Because the filter's gain at zero frequency equals one, the average output values equal the respective average input values.
Solution to Exercise 4.8.1
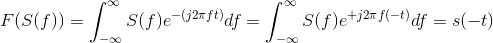
Solution to Exercise 4.8.2
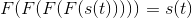 . We know that F (S (f)) =
. We know that F (S (f)) =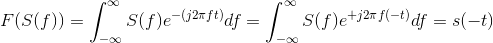 s (−t). Therefore, two Fourier transforms applied to s (t) yields s
(−t). We need two more to get us back where we started.
s (−t). Therefore, two Fourier transforms applied to s (t) yields s
(−t). We need two more to get us back where we started.
Solution to Exercise 4.8.3
The signal is the inverse Fourier transform of the triangularly shaped spectrum, and equals

Solution to Exercise 4.8.4
The result is most easily found in the spectrum's formula: the power in the signal-related part of x (t) is half the power of the signal s (t).
Solution to Exercise 4.9.1
The inverse transform of the frequency response is 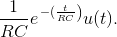 Multiplying the frequency response by
Multiplying the frequency response by 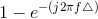 means subtract from the original signal its time-delayed version. response's time-domain version by Δ results in RC eu (t − Δ).
Delaying the frequency resonse’s time-domain version byΔ results in
means subtract from the original signal its time-delayed version. response's time-domain version by Δ results in RC eu (t − Δ).
Delaying the frequency resonse’s time-domain version byΔ results in 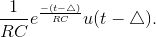 Subtracting from the undelayed signal
Subtracting from the undelayed signal 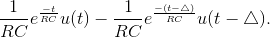 Now
we integrate this sum. Because the integral of a sum equals the sum of the component integrals (integration is linear), we can consider each separately. Because integration and signal-delay are
linear, the integral of a delayed signal equals the delayed version of the integral. The integral is provided in the example.
Now
we integrate this sum. Because the integral of a sum equals the sum of the component integrals (integration is linear), we can consider each separately. Because integration and signal-delay are
linear, the integral of a delayed signal equals the delayed version of the integral. The integral is provided in the example.
Solution to Exercise 4.10.1
If the glottis were linear, a constant input (a zero-frequency sinusoid) should yield a constant output. The periodic output indicates nonlinear behavior.
Solution to Exercise 4.10.2
In the bottom-left panel, the period is about 0.009 s, which equals a frequency of 111 Hz. The bottom-right panel has a period of about 0.0065 s, a frequency of 154 Hz.
Solution to Exercise 4.10.3
Because males have a lower pitch frequency, the spacing between spectral lines is smaller. This closer spacing more accurately reveals the formant structure. Doubling the pitch frequency to 300 Hz for Figure 4.16 (voice spectrum) would amount to removing every other spectral line.
- 瀏覽次數:8736






