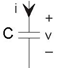
The capacitor stores charge and the relationship between the charge stored and the resultant voltage is q = Cv. The constant of proportionality, the capacitance, has units of farads (F), and is named for the English experimental physicist Michae l Faraday. As current is the rate of change of charge, the v-i relation can be expressed in differential or integral form.
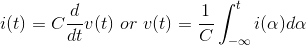
If the voltage across a capacitor is constant, then the current flowing into it equals zero. In this situation, the capacitor is equivalent to an open circuit. The power consumed/produced by a voltage applied to a capacitor depends on the product of the voltage and its derivative.
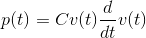
This result means that a capacitor's total energy expenditure up to time t is concisely given by
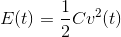
This expression presumes the fundamental assumption of circuit theory: all voltages and currents in any circuit were zero in the far distant past (t = −∞).
- 2164 reads






