When we find the differential equation relating the source and the output, we are faced with solving the circuit in what is known as the time domain. What we emphasize here is that it is often easier to find the output if we use impedances. Because impedances depend only on frequency, we find ourselves in the frequency domain. A common error in using impedances is keeping the time-dependent part, the complex exponential, in the fray. The entire point of using impedances is to get rid of time and concentrate on frequency. Only after we find the result in the frequency domain do we go back to the time domain and put things back together again.
To illustrate how the time domain, the frequency domain and impedances ft together, consider the time domain and frequency domain to be two work rooms. Since you can't be two places at the same time, you are faced with solving your circuit problem in one of the two rooms at any point in time. Impedances and complex exponentials are the way you get between the two rooms. Security guards make sure you don't try to sneak time domain variables into the frequency domain room and vice versa. Figure 3.25 (Two Rooms) shows how this works.
Two Rooms
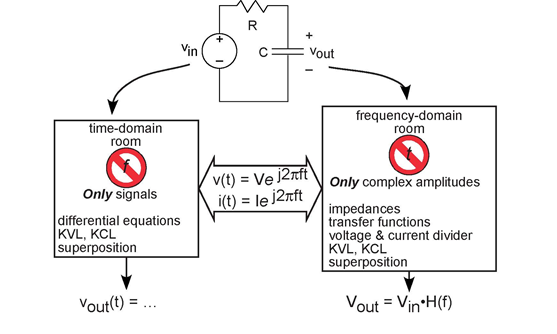
As we unfold the impedance story, we'll see that the powerful use of impedances suggested by Steinmetz greatly simplifies solving circuits, alleviates us from solving differential equations, and suggests a general way of thinking about circuits. Because of the importance of this approach, let's go over how it works.
- Even though it's not, pretend the source is a complex exponential. We do this because the impedance approach simplifies finding how input and output are related. If it were a voltage
source having voltage vin = p (t) (a pulse), still let
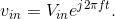 We'll learn how to "get the pulse back" later.
We'll learn how to "get the pulse back" later.
- With a source equaling a complex exponential, all variables in a linear circuit will also be complex exponentials having the same frequency. The circuit's only remaining "mystery" is what each variable's complex amplitude might be. To find these, we consider the source to be a complex number (Vin here) and the elements to be impedances.
- We can now solve using series and parallel combination rules how the complex amplitude of any variable relates to the sources complex amplitude.
Example 3.3
To illustrate the impedance approach, we refer to the RC circuit (Figure 3.26 (Simple Circuits)) below, and we assume that  .
.
Simple Circuits
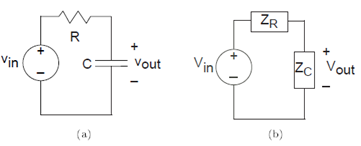
Using impedances, the complex amplitude of the output voltage Vout can be found using voltage divider:
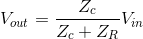
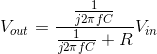
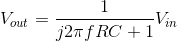
If we refer to the differential equation for this circuit (shown in Circuits with Capacitors and Inductors (Section 3.8) to be 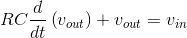 , letting the output and input voltages be complex exponentials, we obtain the same relationship
between their complex amplitudes. Thus, using impedances is equivalent to using the differential equation and solving it when the source is a complex exponential.
, letting the output and input voltages be complex exponentials, we obtain the same relationship
between their complex amplitudes. Thus, using impedances is equivalent to using the differential equation and solving it when the source is a complex exponential.
In fact, we can find the differential equation directly using impedances. If we cross-multiply the relation between input and output amplitudes,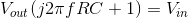
and then put the complex exponentials back in, we have
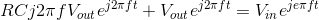
In the process of defining impedances, note that the factor j2πf arises from the derivative of a complex exponential. We can reverse the impedance process, and revert back to the differential equation.
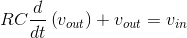
This is the same equation that was derived much more tediously in Circuits with Capacitors and Inductors (Section 3.8). Finding the differential equation relating output to input is far simpler when we use impedances than with any other technique.
Exercise 3.10.1
Suppose you had an expression where a complex amplitude was divided by j2πf. What time-domain operation corresponds to this division?
- 3856 reads






