Solution to Exercise 3.1.1
One kilowatt-hour equals 3,600,000 watt-seconds, which indeed directly corresponds to 3,600,000 joules.
Solution to Exercise 3.4.1
KCL says that the sum of currents entering or leaving a node must be zero. If we consider two nodes together as a "supernode", KCL applies as well to currents entering the combination. Since no currents enter an entire circuit, the sum of currents must be zero. If we had a two-node circuit, the KCL equation of one must be the negative of the other, We can combine all but one node in a circuit into a supernode; KCL for the supernode must be the negative of the remaining node's KCL equation. Consequently, specifying n − 1 KCL equations always specifies the remaining one.
Solution to Exercise 3.4.2
The circuit serves as an amplifier having a gain of 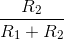
Solution to Exercise 3.5.1
The power consumed by the resistor R1 can be expressed as
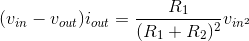
Solution to Exercise 3.5.2
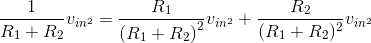
Solution to Exercise 3.6.1
Replacing the current source by a voltage source does not change the fact that the voltages are identical.
Consequently, 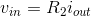 or
or 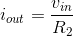 . This result does not depend on the resistor R1, which means that we simply have a resistor (R2) across a voltage source. The two-resistor circuit has no apparent use.
. This result does not depend on the resistor R1, which means that we simply have a resistor (R2) across a voltage source. The two-resistor circuit has no apparent use.
Solution to Exercise 3.6.2
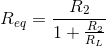 . Thus, a 10% change means that the ratio
. Thus, a 10% change means that the ratio 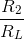 must be less than 0.1. A 1% change means that
must be less than 0.1. A 1% change means that
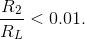
Solution to Exercise 3.6.3
In a series combination of resistors, the current is the same in each; in a parallel combination, the voltage is the same. For a series combination, the equivalent resistance is the sum of the resistances, which will be larger than any component resistor's value; for a parallel combination, the equivalent conductance is the sum of the component conductances, which is larger than any component conductance. The equivalent resistance is therefore smaller than any component resistance.
Solution to Exercise 3.7.1
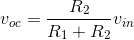 and
and 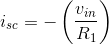 (resistor R2 is shorted out in this case) . Thus,
(resistor R2 is shorted out in this case) . Thus, 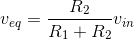 and
and 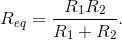
Solution to Exercise 3.7.2
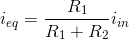 and
and 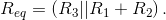 .
.
Solution to Exercise 3.10.1
Division by j2πf arises from integrating a complex exponential. Consequently,
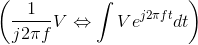
Solution to Exercise 3.11.1
For maximum power dissipation, the imaginary part of complex power should be zero. As the complex power is given by VI * = |V ||I|ej(φ−θ), zero imaginary part occurs when the phases of the voltage and currents agree.
Solution to Exercise 3.11.2
Pave = Vrms Irmscos (φ − θ). The cosine term is known as the power factor.
Solution to Exercise 3.13.1
The key notion is writing the imaginary part as the difference between a complex exponential and its complex conjugate:
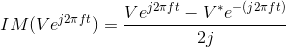
The response to Vej2πft is VH (f) ej2πft, which means the response to V* e-(j2πft) is V*H (−f) e-(j2πft).
As H(-f) = (H (f)*), the Superposition Principle says that the output to the imaginary part is Im (VH (f) ej2πft). The same argument holds for the real part: Re(V ej2πft) → Re (VH (f) ej2πft).
Solution to Exercise 3.15.1
To find the equivalent resistance, we need to find the current flowing through the voltage source. This current equals the current we have just found plus the current flowing through the other
vertical 1 Ω resistor. This current equals 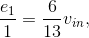 making the
total current through the voltage source (flowing out of it)
making the
total current through the voltage source (flowing out of it) 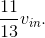 .
.
Thus, the equivalent resistance is 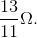
Solution to Exercise 3.15.2
Not necessarily, especially if we desire individual knobs for adjusting the gain and the cutoff frequency.
Solution to Exercise 3.19.1
The ratio between adjacent values is about 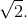
- 4644 reads






