The classic Fourier series as derived originally expressed a periodic signal (period T ) in terms of harmonically related sines and cosines.
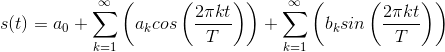
The complex Fourier series and the sine-cosine series are identical, each representing a signal's spectrum. The Fourier coefficients, ak and bk, express the real and imaginary parts respectively of the spectrum while the coefficients ck of the complex Fourier series express the spectrum as a magnitude and phase. Equating the classic Fourier series (4.11) to the complex Fourier series (4.1), an extra factor of two and complex conjugate become necessary to relate the Fourier coefficients in each.
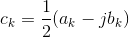
Exercise 4.3.1
Derive this relationship between the coefficients of the two Fourier series. Just as with the complex Fourier series, we can find the Fourier coefficients using the orthogonally properties of sinusoids. Note that the cosine and sine of harmonically related frequencies, even the same frequency, are orthogonal.
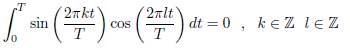
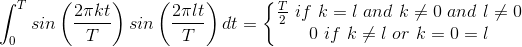
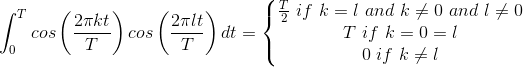
These orthogonality relations follow from the following important trigonometric identities.
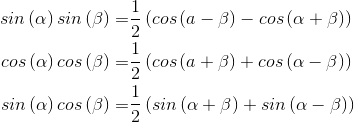
These identities allow you to substitute a sum of sines and/or cosines for a product of them. Each term in the sum can be integrated by noticing one of two important properties of sinusoids.
- The integral of a sinusoid over an integer number of periods equals zero.
- The integral of the square of a unit-amplitude sinusoid over a period T equals
 .
.
To use these, let's, for example, multiply the Fourier series for a signal by the cosine of the lth harmonic 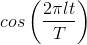 and integrate. The idea is that, because integration is
linear, the integration will sift out all but the term involving al.
and integrate. The idea is that, because integration is
linear, the integration will sift out all but the term involving al.
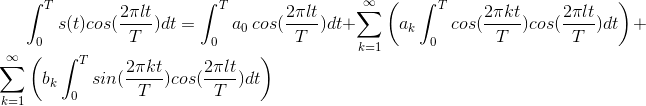
The first and third terms are zero; in the second, the only non-zero term in the sum results when the indices k and l are equal (but not zero), in which case we obtain 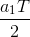 . If k =0= l, we obtain a0T . Consequently,
. If k =0= l, we obtain a0T . Consequently,
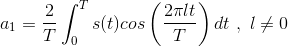
All of the Fourier coefficients can be found similarly.
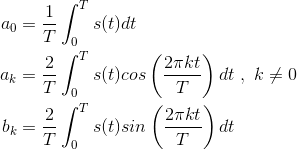
Exercise 4.3.2
The expression for a0 is referred to as the average value of s(t). Why?
Exercise 4.3.3
What is the Fourier series for a unit-amplitude square wave?
Example 4.2
Let's find the Fourier series representation for the half-wave rectified sinusoid.
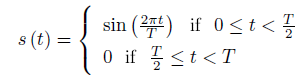
Begin with the sine terms in the series; to find bk we must calculate the integral
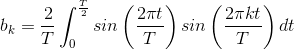
Using our trigonometric identities turns our integral of a product of sinusoids into a sum of integrals of individual sinusoids, which are much easier to evaluate.
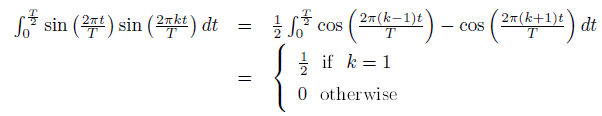
Thus,
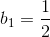
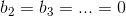
On to the cosine terms. The average value, which corresponds to a0, equals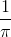 . The remainder of the cosine coefficients are easy to fnd, but yield the complicated result
. The remainder of the cosine coefficients are easy to fnd, but yield the complicated result
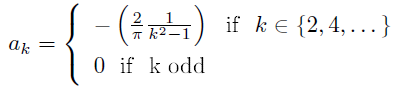
Thus, the Fourier series for the half-wave rectified sinusoid has non-zero terms for the average, the fundamental, and the even harmonics.
- 4217 reads






