Solutions to Exercises in Chapter 4

Available under Creative Commons-ShareAlike 4.0 International License.

Solution to Exercise 4.2.1

Because of Euler's relation,

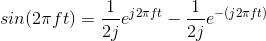
$sin(2\pi ft)=\frac{1}{2j}e^{j2\pi ft}-\frac{1}{2j}e^{-(j2\pi ft)}$

Thus, 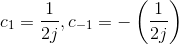$c_1=\frac{1}{2j},c_{-1}=-\left ( \frac{1}{2j \right )}$ , and the other coefficients are zero.

Solution to Exercise 4.2.2

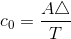$c_0=\frac{A\triangle}{T}$ . This quantity clearly corresponds to the periodic pulse signal's average value.

Solution to Exercise 4.3.1

Write the coefficients of the complex Fourier series in Cartesian form as c_k = A_k + jB_k and substitute into the expression for the complex Fourier series.

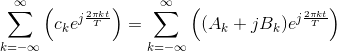
$\sum_{k=-\infty }^{\infty }\left ( c_ke^{j\frac{2\pi kt}{T} \right )}=\sum_{k=-\infty }^{\infty }\left ( (A_k +jB_k)e^{j\frac{2\pi kt}{T} \right )}$

Simplifying each term in the sum using Euler’s formula.

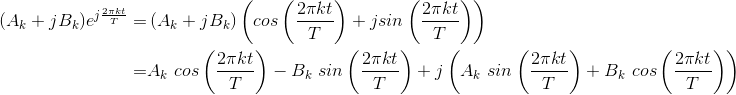
$\begin{align*} (A_k+jB_k)e^{j\frac{2\pi kt}{T}}=&\left ( A_k+jB_k \right )\left ( cos\left ( \frac{2\pi kt}{T} \right )+jsin\left ( \frac{2\pi kt}{T} \right ) \right )\\ =&A_k\ cos\left ( \frac{2\pi kt}{T} \right )-B_k\ sin\left ( \frac{2\pi kt}{T} \right )+j\left ( A_k\ sin\left ( \frac{2\pi kt}{T} \right ) +B_k\ cos\left ( \frac{2\pi kt}{T} \right )\right )\\ \end{align*}$

We now combine terms that have the same frequency index in magnitude. Because the signal is real-valued, the coefficients of the complex Fourier series have conjugate symmetry: c_−k = c_k*or A_−k = A_k and B_−k = −B_k. After we add the positive-indexed and negative-indexed terms, each term in the Fourier series becomes 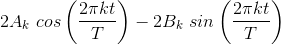$2A_k\ cos\left ( \frac{2\pi kt}{T} \right )-2B_k\ sin\left ( \frac{2\pi kt}{T} \right )$ . To obtain the classic Fourier series (4.11), we must have 2A_k= a_kand 2B_k = −b_k.

Solution to Exercise 4.3.2

The average of a set of numbers is the sum divided by the number of terms. Viewing signal integration as the limit of a Riemann sum, the integral corresponds to the average.

Solution to Exercise 4.3.3

We found that the complex Fourier series coefficients are given by 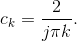$c_k=\frac{2}{j\pi k}.$ The coefficients are pure imaginary, which means a_k =0. The coefficients of the sine terms are given by b_k = − (2Im (c_k)) so that

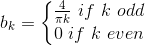
$\begin{align*} b_{k}=\left\{\begin{matrix} \frac{4}{\pi k}\ if\ k\ odd & \\ 0\ if\ k\ even & \end{matrix}\right. \end{align*}$

Thus, the Fourier series for the square wave is

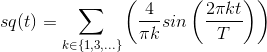
$sq(t)=\sum_{k\in \left \{ 1,3,... \right \}}^{ }\left ( \frac{4}{\pi k}sin\left ( \frac{2\pi kt}{T} \right ) \right )$

Solution to Exercise 4.4.1

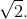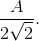The rms value of a sinusoid equals its amplitude divided by $\sqrt{2}.$ As a half-wave rectified sine wave is zero during half of the period, its rms value is $\frac{A}{2\sqrt{2}}.$ since the integral of the squared half-wave rectified sine wave equals half that of a squared sinusoid.

Solution to Exercise 4.4.2

Total harmonic distortion equals 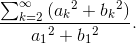$\frac{\sum_{k=2}^{\infty }\left ( a{_{k}}^{2}+b{_{k}}^{2} \right )}{a{_{1}}^{2}+b{_{1}}^{2}}.$ Clearly, this quantity is most easily computed in the frequency domain. However, the numerator equals the square of the signal's rms value minus the power in the average and the power in the first harmonic.

Solution to Exercise 4.5.1

Total harmonic distortion in the square wave is 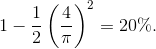$1-\frac{1}{2}\left ( \frac{4}{\pi } \right )^{2}=20 \%.$

Solution to Exercise 4.6.1

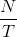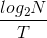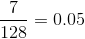N signals directly encoded require a bandwidth of $\frac{N}{T}$ . Using a binary representation, we need $\frac{log_2N}{T}$ . For N = 128, the binary-encoding scheme has a factor of $\frac{7}{128}=0.05$ smaller bandwidth. Clearly, binary encoding is superior.

Solution to Exercise 4.6.2

We can use N different amplitude values at only one frequency to represent the various letters.

Solution to Exercise 4.7.1

Because the filter's gain at zero frequency equals one, the average output values equal the respective average input values.

Solution to Exercise 4.8.1

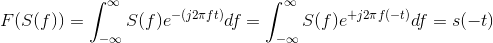
$F(S(f))=\int_{-\infty }^{\infty }S(f)e^{-(j2\pi ft)}df=\int_{-\infty }^{\infty }S(f)e^{+j2\pi f(-t)}df=s(-t)$

Solution to Exercise 4.8.2

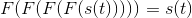F(F(F(F(s(t)))))=s(t) . We know that F (S (f)) = 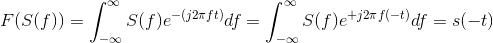$F(S(f))=\int_{-\infty }^{\infty }S(f)e^{-(j2\pi ft)}df=\int_{-\infty }^{\infty }S(f)e^{+j2\pi f(-t)}df=s(-t)$ s (−t). Therefore, two Fourier transforms applied to s (t) yields s (−t). We need two more to get us back where we started.

Solution to Exercise 4.8.3

The signal is the inverse Fourier transform of the triangularly shaped spectrum, and equals

$s\left ( t \right )=W\left ( \frac{sin(\left \pi Wt \right )}{\pi W t} \right )^2$

Solution to Exercise 4.8.4

The result is most easily found in the spectrum's formula: the power in the signal-related part of x (t) is half the power of the signal s (t).

Solution to Exercise 4.9.1

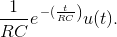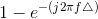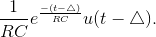The inverse transform of the frequency response is $\frac{1}{RC}e^{\left -( \frac{t}{RC} \right )}u(t).$ Multiplying the frequency response by $1-e^{-(j2\pi f\triangle)}$ means subtract from the original signal its time-delayed version. response's time-domain version by Δ results in RC eu (t − Δ). Delaying the frequency resonse’s time-domain version byΔ results in $\frac{1}{RC}e^{\frac{-(t-\triangle)}{RC}}u(t-\triangle).$ Subtracting from the undelayed signal 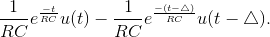$\frac{1}{RC}e^{\frac{-t}{RC}}u(t)-\frac{1}{RC}e^{\frac{-(t-\triangle)}{RC}}u(t-\triangle).$ Now we integrate this sum. Because the integral of a sum equals the sum of the component integrals (integration is linear), we can consider each separately. Because integration and signal-delay are linear, the integral of a delayed signal equals the delayed version of the integral. The integral is provided in the example.

Solution to Exercise 4.10.1

If the glottis were linear, a constant input (a zero-frequency sinusoid) should yield a constant output. The periodic output indicates nonlinear behavior.

Solution to Exercise 4.10.2

In the bottom-left panel, the period is about 0.009 s, which equals a frequency of 111 Hz. The bottom-right panel has a period of about 0.0065 s, a frequency of 154 Hz.

Solution to Exercise 4.10.3

Because males have a lower pitch frequency, the spacing between spectral lines is smaller. This closer spacing more accurately reveals the formant structure. Doubling the pitch frequency to 300 Hz for Figure 4.16 (voice spectrum) would amount to removing every other spectral line.

5809 reads

You are here

Solutions to Exercises in Chapter 4