When we consider the much more realistic situation when we have a channel that introduces attenuation and noise, we can make use of the just-described receiver's linear nature to directly derive the receiver's output. The attenuation affects the output in the same way as the transmitted signal: It scales the output signal by the same amount. The white noise, on the other hand, should be filtered from the received signal before demodulation. We must thus insert a bandpass filter having bandwidth 2W and center frequency fc: This filter has no effect on the received signal-related component, but does remove out-of-band noise power. As shown in the triangular-shaped signal spectrum (Figure 6.6), we apply coherent receiver to this filtered signal, with the result that the demodulated output contains noise that cannot be removed: It lies in the same spectral band as the signal.
As we derive the signal-to-noise ratio in the demodulated signal, let's also calculate the signal-to-noise ratio of the bandpass filter's output 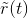 The signal component of
The signal component of 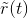 equals αAcm (t) cos (2πfct) . This signal's
Fourier transform equals
equals αAcm (t) cos (2πfct) . This signal's
Fourier transform equals
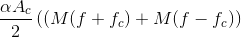
(6.33)
making the power spectrum,
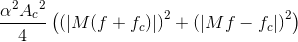
(6.34)
Exercise 6.12.1
If you calculate the magnitude-squared of the first equation, you don't obtain the second unless you make an assumption. What is it?
Thus, the total signal-related power in 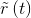 is
is 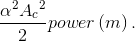 The noise power equals the integral of
the noise power spectrum; because the power spectrum is constant over the transmission band, this integral equals the noise amplitude N0 times the filter's bandwidth
2W . The so-called received signal-to-noise ratio the signal-to-noise ratio after the de rigeur front-end bandpass filter and before demodulation equals
The noise power equals the integral of
the noise power spectrum; because the power spectrum is constant over the transmission band, this integral equals the noise amplitude N0 times the filter's bandwidth
2W . The so-called received signal-to-noise ratio the signal-to-noise ratio after the de rigeur front-end bandpass filter and before demodulation equals
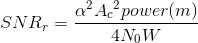
(6.35)
The demodulated signal 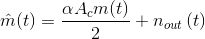 Clearly, the signal power equals
Clearly, the signal power equals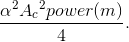 To determine the noise power, we must understand how the coherent demodulator afects the bandpass noise found in
To determine the noise power, we must understand how the coherent demodulator afects the bandpass noise found in 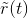 Because we are concerned with noise, we must deal with the power spectrum
since we don't have the Fourier transform available to us. Letting P (f) denote the power spectrum of
Because we are concerned with noise, we must deal with the power spectrum
since we don't have the Fourier transform available to us. Letting P (f) denote the power spectrum of 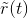 's noise component, the power spectrum after multiplication by the carrier has the form
's noise component, the power spectrum after multiplication by the carrier has the form
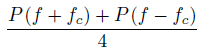 (6.36)
(6.36)
The delay and advance in frequency indicated here results in two spectral noise bands falling in the low-frequency region of lowpass filter's passband. Thus, the total noise power in this
filter's output equals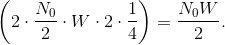 The signal-to-noise ratio of the receiver's output thus equals
The signal-to-noise ratio of the receiver's output thus equals
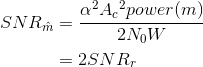
(6.37)
Let's break down the components of this signal-to-noise ratio to better appreciate how the channel and the transmitter parameters affect communications performance. Better performance, as measured by the SNR, occurs as it increases.
- More transmitter power increasing AC increases the signal-to-noise ratio proportionally.
- The carrier frequency fc has no effect on SNR, but we have assumed that fc » W .
- The signal bandwidth W enters the signal-to-noise expression in two places: implicitly through the signal power and explicitly in the expression's denominator. If the signal spectrum had a constant amplitude as we increased the bandwidth, signal power would increase proportionally. On the other hand, our transmitter enforced the criterion that signal amplitude was constant (Communication with Satellites). Signal amplitude essentially equals the integral of the magnitude of the signal's spectrum.
NOTE: This result isn't exact, but we do know that
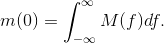
Enforcing the signal amplitude specification means that as the signal's bandwidth increases we must decrease the spectral amplitude, with the result that the signal power remains constant. Thus, increasing signal bandwidth does indeed decrease the signal-to-noise ratio of the receiver's output.
- Increasing channel attenuation moving the receiver farther from the transmitter decreases the signal-to-noise ratio as the square. Thus, signal-to-noise ratio decreases as distance-squared between transmitter and receiver.
- Noise added by the channel adversely affects the signal-to-noise ratio.
In summary, amplitude modulation provides an effective means for sending a bandlimited signal from one place to another. For wireline channels, using baseband or amplitude modulation makes little difference in terms of signal-to-noise ratio. For wireless channels, amplitude modulation is the only alternative. The one AM parameter that does not affect signal-to-noise ratio is the carrier frequency fc: We can choose any value we want so long as the transmitter and receiver use the same value. However, suppose someone else wants to use AM and chooses the same carrier frequency. The two resulting transmissions will add, and both receivers will produce the sum of the two signals. What we clearly need to do is talk to the other party, and agree to use separate carrier frequencies. As more and more users wish to use radio, we need a forum for agreeing on carrier frequencies and on signal bandwidth. On earth, this forum is the government. In the United States, the Federal Communications Commission (FCC) strictly controls the use of the electromagnetic spectrum for communications. Separate frequency bands are allocated for commercial AM, FM, cellular telephone (the analog version of which is AM), short wave (also AM), and satellite communications.
Exercise 6.12.2
Suppose all users agree to use the same signal bandwidth. How closely can the carrier frequencies be while avoiding communications crosstalk? What is the signal bandwidth for commercial AM? How does this bandwidth compare to the speech bandwidth?
- 13560 reads






