If E > C, the probability of an error in a decoded block must approach one regardless of the code that might be chosen.
![\lim _{N\rightarrow \infty }Pr\left [Block\: error \right ]=1](/system/files/resource/9/9648/9800/media/eqn-img_1.gif)
(6.59)
These results mean that it is possible to transmit digital information over a noisy channel (one that introduces errors) and receive the information without error if the code is sufficiently inefficient compared to the channel's characteristics. Generally, a channel's capacity changes with the signal-to-noise ratio: As one increases or decreases, so does the other. The capacity measures the overall error characteristics of a channel the smaller the capacity the more frequently errors occur and an overly efficient error-correcting code will not build in enough error correction capability to counteract channel errors.
This result astounded communication engineers when Shannon published it in 1948. Analog communication always yields a noisy version of the transmitted signal; in digital communication, error correction can be powerful enough to correct all errors as the block length increases. The key for this capability to exist is that the code's efficiency be less than the channel's capacity. For a binary symmetric channel, the capacity is given by
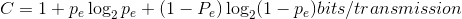
(6.60)
Figure 6.24 (capacity of a channel) shows how capacity varies with error probability. For example, our (7,4) Hamming code has an efficiency of 0.57, and codes having the same efciency but longer block sizes can be used on additive noise channels where the signal-to-noise ratio exceeds 0dB.

The capacity per transmission through a binary symmetric channel is plotted as a function of the digital channel's error probability (upper) and as a function of the signal-to-noise ratio for a BPSK signal set (lower).
- 2856 reads






