Euler's Formula

Available under Creative Commons-ShareAlike 4.0 International License.

Surprisingly, the polar form of a complex number z can be expressed mathematically as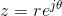 $z = re^{j\theta }$

To show this result, we use Euler's relations that express exponentials with imaginary arguments in terms of trigonometric functions.

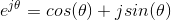
$e^{j\theta}=cos(\theta)+jsin(\theta)$
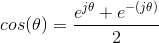
$cos(\theta)=\frac{e^{j\theta}+e^{-(j\theta)}}{2}$
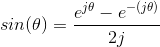
$sin(\theta)=\frac{e^{j\theta}-e^{-(j\theta)}}{2j}$

The first of these is easily derived from the Taylor's series for the exponential.

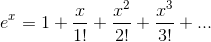
$e^{x}=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...$

Substituting jθ for x, we find that

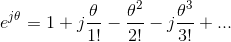
$e^{j\theta}=1+j\frac{\theta}{1!}-\frac{\theta^2}{2!}-j\frac{\theta^3}{3!}+...$

because j² = −1, j³ = −j, and j⁴ =1. Grouping separately the real-valued terms and the imaginary-valued ones,

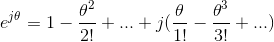
$e^{j\theta}=1-\frac{\theta^2}{2!}+...+j(\frac{\theta}{1!}-\frac{\theta^3}{3!}+...)$

The real-valued terms correspond to the Taylor's series for cos (θ), the imaginary ones to sin (θ), and Euler's first relation results. The remaining relations are easily derived from the first. We see that multiplying the exponential in (2.3) by a real constant corresponds to setting the radius of the complex number to the constant.

2017 reads

You are here

Euler's Formula