Imagine that you have taken all of the samples with n=10 from a population that you knew the mean of, found the t-distribution for 9 df by computing a t-score for each sample and generated a
relative frequency distribution of the t's. When you were finished, someone brought you another sample (n=10) wondering if that new sample came from the original population. You could use your
sampling distribution of t's to test if the new sample comes from the original population or not. To conduct the test, first hypothesize that the new sample comes from the original population.
With this hypothesis, you have hypothesized a value for 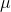 , the mean
of the original population, to use to compute a t-score for the new sample. If the t for the new sample is close to zero—if the t-score for the new sample could easily have come from the middle
of the t-distribution you generated—your hypothesis that the new sample comes from a population with the hypothesized mean seems reasonable and you can conclude that the data supports the new
sample coming from the original population. If the t-score from the new sample was far above or far below zero, your hypothesis that this new sample comes from the original population seems
unlikely to be true, for few samples from the original population would have t-scores far from zero. In that case, conclude that the data gives support to the idea that the new sample comes
from some other population.
, the mean
of the original population, to use to compute a t-score for the new sample. If the t for the new sample is close to zero—if the t-score for the new sample could easily have come from the middle
of the t-distribution you generated—your hypothesis that the new sample comes from a population with the hypothesized mean seems reasonable and you can conclude that the data supports the new
sample coming from the original population. If the t-score from the new sample was far above or far below zero, your hypothesis that this new sample comes from the original population seems
unlikely to be true, for few samples from the original population would have t-scores far from zero. In that case, conclude that the data gives support to the idea that the new sample comes
from some other population.
This is the basic method of using this t-test. Hypothesize the mean of the population you think a sample might come from. Using that mean, compute the t-score for the sample. If the t-score is close to zero, conclude that your hypothesis was probably correct and that you know the mean of the population from which the sample came. If the t-score is far from zero, conclude that your hypothesis is incorrect, and the sample comes from a population with a different mean.
Once you understand the basics, the details can be filled in. The details of conducting a "hypothesis test of the population mean", testing to see if a sample comes from a population with a certain mean—are of two types. The first type concerns how to do all of this in the formal language of statisticians. The second type of detail is how to decide what range of t-scores implies that the new sample comes from the original population.
You should remember from the last chapter that the formal language of hypothesis testing always requires two hypotheses. The first hypothesis is called the "null hypothesis", usually denoted
H0 :. It states that there is no difference between the mean of the population from which the sample is drawn and the hypothesized mean. The second is the "alternative
hypothesis", denoted H1 : or Ha :. It states that the mean of the population from which the sample comes is different from the hypothesized value. If
your question is simply "does this sample come from a population with this mean?", your Ha : is simply 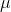 ≠ the hypothesized value . If your question is "does this
sample come from a population with a mean greater than some value”, then your Ha : becomes
≠ the hypothesized value . If your question is "does this
sample come from a population with a mean greater than some value”, then your Ha : becomes 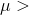 the hypothesized value .
the hypothesized value .
The other detail is deciding how "close to zero" the sample t-score has to be before you conclude that the null hypothesis is probably correct. How close to zero the sample t-score must be
before you conclude that the data supports H0 : depends on the df and how big a chance you want to take that you will make a mistake. If you decide to conclude that the
sample comes from a population with the hypothesized mean only if the sample t is very, very close to zero, there are many samples actually from the population that will have t-scores that
would lead you to believe they come from a population with some other mean—it would be easy to make a mistake and conclude that these samples come from another population. On the other hand, if
you decide to accept the null hypothesis even if the sample t-score is quite far from zero, you will seldom make the mistake of concluding that a sample from the original population is from
some other population, but you will often make another mistake — concluding that samples from other populations are from the original population. There are no hard rules for deciding how much
of which sort of chance to take. Since there is a trade-off between the chance of making the two different mistakes, the proper amount of risk to take will depend on the relative costs of the
two mistakes. Though there is no firm basis for doing so, many researchers use a 5 per cent chance of the first sort of mistake as a default. The level of chance of making the first error is
usually called "alpha" ( 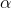 ) and the value of alpha chosen is
usually written as a decimal fraction—taking a 5 per cent chance of making the first mistake would be stated as "
) and the value of alpha chosen is
usually written as a decimal fraction—taking a 5 per cent chance of making the first mistake would be stated as " 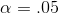 ". When in doubt, use
". When in doubt, use 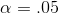 .
.
If your alternative hypothesis is "not equal to", you will conclude that the data supports Ha : if your sample t-score is either well below or well above zero and you need
to divide α between the two tails of the t-distribution. If you want to use 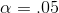 , you will support Ha : if the t is in either the lowest .025 or the highest .025 of the distribution. If
your alternative is "greater than", you will conclude that the data supports Ha : only if the sample t-score is well above zero. So, put all of your α in the right tail.
Similarly, if your alternative is "less than", put the whole α in the left tail.
, you will support Ha : if the t is in either the lowest .025 or the highest .025 of the distribution. If
your alternative is "greater than", you will conclude that the data supports Ha : only if the sample t-score is well above zero. So, put all of your α in the right tail.
Similarly, if your alternative is "less than", put the whole α in the left tail.
The table itself can be confusing even after you know how many degrees of freedom you have and if you want to split your α between the two tails or not. Adding to the confusion, not all
t-tables look exactly the same. Look at the typical t-table above and notice that it has three parts: column headings of decimal fractions, row headings of whole numbers, and a body of numbers
generally with values between 1 and 3. The column headings are labeled p or "area in the right tail," and sometimes are labeled “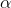 .” The row headings are labeled "df," but are sometimes labeled “ν” or "degrees of freedom". The body is usually left
unlabeled and it shows the t-score which goes with the "
.” The row headings are labeled "df," but are sometimes labeled “ν” or "degrees of freedom". The body is usually left
unlabeled and it shows the t-score which goes with the " 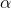 " and
"degrees of freedom" of that column and row. These tables are set up to be used for a number of different statistical tests, so they are presented in a way that is a compromise between ease of
use in a particular situation and the ability to use the same table for a wide variety of tests. My favorite t tables are available online at
" and
"degrees of freedom" of that column and row. These tables are set up to be used for a number of different statistical tests, so they are presented in a way that is a compromise between ease of
use in a particular situation and the ability to use the same table for a wide variety of tests. My favorite t tables are available online at
http://www.itl.nist.gov/div898/handbook/eda/section3/eda3672.htm
In order to use the table to test to see if "this sample comes from a population with a certain mean" choose 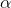 and find the number of degrees of freedom. The number of degrees of freedom in a test involving one sample mean is simply the
size of the sample minus one (df = n-1). The
and find the number of degrees of freedom. The number of degrees of freedom in a test involving one sample mean is simply the
size of the sample minus one (df = n-1). The 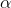 you choose may not
be the
you choose may not
be the 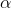 in the column heading. The column headings show the
"right tail areas"—the chance you'll get a t-score larger than the one in the body of the table. Assume that you had a sample with ten members and chose
in the column heading. The column headings show the
"right tail areas"—the chance you'll get a t-score larger than the one in the body of the table. Assume that you had a sample with ten members and chose 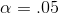 . There are nine degrees of freedom, so go across the 9 df row to the .025 column since
this is a two-tail test, and find the t-score of 2.262. This means that in any sampling distribution of t-scores, with samples of ten drawn from a normal population, only 2.5 per cent (.025) of
the samples would have t-scores greater than 2.262—any t-score greater than 2.262 probably occurs because the sample is from some other population with a larger mean. Because the
t-distributions are symmetrical, it is also true that only 2.5 per cent of the samples of ten drawn from a normal population will have t-scores less than -2.262. Putting the two together, 5 per
cent of the t-scores will have an absolute value greater the 2.262. So if you choose
. There are nine degrees of freedom, so go across the 9 df row to the .025 column since
this is a two-tail test, and find the t-score of 2.262. This means that in any sampling distribution of t-scores, with samples of ten drawn from a normal population, only 2.5 per cent (.025) of
the samples would have t-scores greater than 2.262—any t-score greater than 2.262 probably occurs because the sample is from some other population with a larger mean. Because the
t-distributions are symmetrical, it is also true that only 2.5 per cent of the samples of ten drawn from a normal population will have t-scores less than -2.262. Putting the two together, 5 per
cent of the t-scores will have an absolute value greater the 2.262. So if you choose 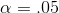 , you will probably be using a t-score in the .025 column. The picture that is at the top of most t-tables shows what is going
on. Look at it when in doubt.
, you will probably be using a t-score in the .025 column. The picture that is at the top of most t-tables shows what is going
on. Look at it when in doubt.
LaTonya Williams is the plant manager for Eileen's Dental Care Company (EDC) which makes dental floss. EDC has a good, stable work force of semi-skilled workers who work packaging floss, paid by piece-work, and the company wants to make sure that these workers are paid more than the local average wage. A recent report by the local Chamber of Commerce shows an average wage for "machine operators" of USD 8.71. LaTonya needs to decide if a raise is needed to keep her workers above the average. She takes a sample of workers, pulls their work reports, finds what each one earned last week and divides their earnings by the hours they worked to find average hourly earnings.
That data appears below:
Smith 9.01
Wilson 8.67
Peterson 8.90
Jones 8.45
Gordon 8.88
McCoy 9.13
Bland 8.77
LaTonya wants to test to see if the mean of the average hourly earnings of her workers is greater than USD 8.71. She wants to use a one-tail test because her question is "greater than" not "unequal to". Her hypotheses are:
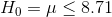 and
and 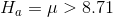
As is usual in this kind of situation, LaTonya is hoping that the data supports Ha :, but she wants to be confident that it does before she decides her workers are
earning above average wages. Remember that she will compute a t-score for her sample using USD 8.71 for 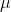 . If her t-score is negative or close to zero, she will conclude that the data supports H0 :. Only if her
t-score is large and positive will she go with Ha :. She decides to use
. If her t-score is negative or close to zero, she will conclude that the data supports H0 :. Only if her
t-score is large and positive will she go with Ha :. She decides to use 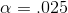 because she is unwilling to take much risk of saying the workers earn above average wages when they really do not. Because her
sample has n=7, she has 6 df. Looking at the table, she sees that the data will support Ha :, the workers earn more than average, only if the sample t-score is
greater than 2.447.
because she is unwilling to take much risk of saying the workers earn above average wages when they really do not. Because her
sample has n=7, she has 6 df. Looking at the table, she sees that the data will support Ha :, the workers earn more than average, only if the sample t-score is
greater than 2.447.
Finding the sample mean and standard deviation, 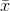 =
$8.83 and s = .225, LaTonya computes her sample t-score:
=
$8.83 and s = .225, LaTonya computes her sample t-score:
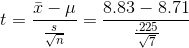
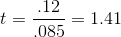
Because her sample t is not greater than +2.447, LaTonya concludes that she will have to raise the piece rates EDC pays in order to be really sure that mean hourly earnings are above the local average wage.
If LaTonya had simply wanted to know if EDC's workers earned the same as other workers in the area, she would have used a two-tail test. In that case her hypotheses would have been:
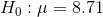 and
and 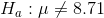
Using 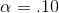 , LaTonya would split the .10 between the two tails
since the data supports Ha : if the sample t-score is either large and negative or large and positive. Her arithmetic is the same, her sample t-score is still 1.41,
but she now will decide that the data supports Ha : only if it is outside ±1.943.
, LaTonya would split the .10 between the two tails
since the data supports Ha : if the sample t-score is either large and negative or large and positive. Her arithmetic is the same, her sample t-score is still 1.41,
but she now will decide that the data supports Ha : only if it is outside ±1.943.
- 1908 reads






