Measuring the shape of a distribution is more difficult. Location has only one dimension ("where?"), but shape has a lot of dimensions. We will talk about two, and you will find that most of the time, only one dimension of shape is measured. The two dimensions of shape discussed here are the width and symmetry of the distribution. The simplest way to measure the width is to do just that—the range in the distance between the lowest and highest members of the population. The range is obviously affected by one or two population members which are much higher or lower than all the rest.
The most common measures of distribution width are the standard deviation and the variance. The standard deviation is simply the square root of the variance, so if you know one (and have a calculator that does squares and square roots) you know the other. The standard deviation is just a strange measure of the mean distance between the members of a population and the mean of the population. This is easiest to see if you start out by looking at the formula for the variance:
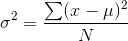
Look at the numerator. To find the variance, the first step (after you have the mean,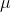 
) is to take each member of the population, and find the difference between its value and the mean; you should have N differences.
Square each of those, and add them together, dividing the sum by N, the number of members of the population. Since you find the mean of a group of things by adding them together and then
dividing by the number in the group, the variance is simply the "mean of the squared distances between members of the population and the population mean".
Notice that this is the formula for a population characteristic, so we use the Greek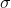 
and that we write the variance as 
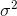, or "sigma square" because the standard deviation is simply the square root of the variance, its symbol is simply "sigma",
.
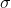One of the things statisticians have discovered is that 75 per cent of the members of any population are within two standard deviations of the mean of the population. This is known as Chebyshev's Theorem. If the mean of a population of shoe sizes is 9.6 and the standard deviation is 1.1, then 75 per cent of the shoe sizes are between 7.4 (two standard deviations below the mean) and 11.8 (two standard deviations above the mean). This same theorem can be stated in probability terms: the probability that anything is within two standard deviations of the mean of its population is .75.
It is important to be careful when dealing with variances and standard deviations. In later chapters, there are formulas using the variance, and formulas using the standard deviation. Be sure you know which one you are supposed to be using. Here again, spreadsheet programs will figure out the standard deviation for you. In Excel, there is a function, =STDEVP(...), that does all of the arithmetic. Most calculators will also compute the standard deviation. Read the little instruction booklet, and find out how to have your calculator do the numbers before you do any homework or have a test.
The other measure of shape we will discuss here is the measure of "skewness". Skewness is simply a measure of whether or not the distribution is symmetric or if it has a long tail on one side, but not the other. There are a number of ways to measure skewness, with many of the measures based on a formula much like the variance. The formula looks a lot like that for the variance, except the distances between the members and the population mean are cubed, rather than squared, before they are added together:
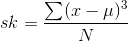
At first it might not seem that cubing rather than squaring those distances would make much difference. Remember, however, that when you square either a positive or negative number you get a
positive number, but that when you cube a positive, you get a positive and when you cube a negative you get a negative. Also remember that when you square a number, it gets larger, but that
when you cube a number, it gets a whole lot larger. Think about a distribution with a long tail out to the left. There are a few members of that population much smaller than the mean, members
for which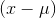 
is large and negative. When these are cubed, you end
up with some really big negative numbers. Because there are not any members with such large, positive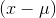 
, there are not any corresponding really big positive numbers to add in when you sum up the 
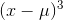, and the sum will be negative. A negative measure of skewness means that there is a tail
out to the left, a positive measure means a tail to the right. Take a minute and convince yourself that if the distribution is symmetric, with equal tails on the left and right, the measure of
skew is zero.
To be really complete, there is one more thing to measure, "kurtosis" or "peakedness". As you might expect by now, it is measured by taking the distances between the members and the mean and raising them to the fourth power before averaging them together.
- 1265 reads
