There are many different types of hypothesis tests, including many that are used more often than the "goodness-of-fit" test. This test will be used to help introduce hypothesis testing because it gives a clear illustration of how the strategy of hypothesis testing is put to use, not because it is used frequently. Follow this example carefully, concentrating on matching the steps described in previous sections with the steps described in this section; the arithmetic is not that important right now.
We will go back to Ann Howard's problem with marketing "Easy Bounce" socks to volleyball teams. Remember that Ann works for Foothills Hosiery, and she is trying to market these sports socks to volleyball teams. She wants to send out some samples to convince volleyball players that wearing "Easy Bounce" socks will be more comfortable than wearing other socks. Her idea is to send out a package of socks to volleyball coaches in the area, so the players can try them out. She needs to include an assortment of sizes in those packages and is trying to find out what sizes to include. The Production Department knows what mix of sizes they currently produce, and Ann has collected a sample of 97 volleyball players' sock sizes from nearby teams. She needs to test to see if her sample supports the hypothesis that volleyball players have the same distribution of sock sizes as Foothills is currently producing—is the distribution of volleyball players' sock sizes a "good fit" to the distribution of sizes now being produced?
Ann's sample, a sample of the sock sizes worn by volleyball players, as a frequency distribution of sizes:
|
size |
frequency |
|
6 |
3 |
|
7 |
24 |
|
8 |
33 |
|
9 |
20 |
|
10 |
17 |
From the Production Department, Ann finds that the current relative frequency distribution of production of "Easy Bounce" socks is like this:
|
size |
re. frequency |
|
6 |
0.06 |
|
7 |
0.13 |
|
8 |
0.22 |
|
9 |
0.3 |
|
10 |
0.26 |
|
11 |
0.03 |
If the world is "unsurprising", volleyball players will wear the socks sized in the same proportions as other athletes, so Ann writes her hypotheses:
H0 : Volleyball players' sock sizes are distributed just like current production.
Ha : Volleyball players' sock sizes are distributed differently.
Ann's sample has n=97. By applying the relative frequencies in the current production mix, she can find out how many players would be "expected" to wear each size if her sample was perfectly representative of the distribution of sizes in current production. This would give her a description of what a sample from the population in the null hypothesis would be like. It would show what a sample that had a "very good fit" with the distribution of sizes in the population currently being produced would look like.
Statisticians know the sampling distribution of a statistic which compares the "expected" frequency of a sample with the actual, or "observed" frequency. For a sample with c different classes
(the sizes here), this statistic is distributed like 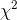 with c-1
df. The
with c-1
df. The 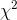 is computed by the formula:
is computed by the formula:
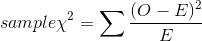
where:
O = observed frequency in the sample in this class
E = expected frequency in the sample in this class.
The expected frequency, E, is found by multiplying the relative frequency of this class in the H0 : hypothesized population by the sample size. This gives you the number in that class in the sample if the relative frequency distribution across the classes in the sample exactly matches the distribution in the population.
Notice that 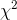 is always ≥ 0 and equals 0 only if the observed is
equal to the expected in each class. Look at the equation and make sure that you see that a larger value of
is always ≥ 0 and equals 0 only if the observed is
equal to the expected in each class. Look at the equation and make sure that you see that a larger value of 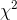 goes with samples with large differences between the observed and expected frequencies.
goes with samples with large differences between the observed and expected frequencies.
Ann now needs to come up with a rule to decide if the data supports H0 : or Ha : . She looks at the table and sees that for 5 df (there
are 6 classes—there is an expected frequency for size 11 socks), only .05 of samples drawn from a given population will have a 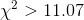 and only .10 will have a
and only .10 will have a 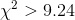 . She decides that it would not be all that surprising if volleyball players had a
different distribution of sock sizes than the athletes who are currently buying "Easy Bounce", since all of the volleyball players are women and many of the current customers are men. As a
result, she uses the smaller .10 value of 9.24 for her decision rule. Now she must compute her sample
. She decides that it would not be all that surprising if volleyball players had a
different distribution of sock sizes than the athletes who are currently buying "Easy Bounce", since all of the volleyball players are women and many of the current customers are men. As a
result, she uses the smaller .10 value of 9.24 for her decision rule. Now she must compute her sample 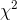 . Ann starts by finding the expected frequency of size 6 socks by multiplying the relative frequency of size 6 in the population
being produced by 97, the sample size. She gets E = .06*97=5.82. She then finds O-E = 3-5.82 = -2.82, squares that and divides by 5.82, eventually getting 1.37. She then realizes that she will
have to do the same computation for the other five sizes, and quickly decides that a spreadsheet will make this much easier. Her spreadsheet looks like this:
. Ann starts by finding the expected frequency of size 6 socks by multiplying the relative frequency of size 6 in the population
being produced by 97, the sample size. She gets E = .06*97=5.82. She then finds O-E = 3-5.82 = -2.82, squares that and divides by 5.82, eventually getting 1.37. She then realizes that she will
have to do the same computation for the other five sizes, and quickly decides that a spreadsheet will make this much easier. Her spreadsheet looks like this:
|
sock size |
frequency in sample |
population relative frequency |
expected frequency = 97*C |
(O-E)^2/E |
|
6 |
3 |
0.06 |
5.82 |
1.3663918 |
|
7 |
24 |
0.13 |
12.61 |
10.288033 |
|
8 |
33 |
0.22 |
21.34 |
6.3709278 |
|
9 |
20 |
0.3 |
29.1 |
2.8457045 |
|
10 |
17 |
0.26 |
25.22 |
2.6791594 |
|
11 |
0 |
0.03 |
2.91 |
2.91 |
|
97 |
26.460217 |
Ann performs her third step, computing her sample statistic, using the spreadsheet. As you can see, her sample 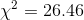 , which is well into the "unusual" range which starts at 9.24 according to her decision rule. Ann has found that her sample data
supports the hypothesis that the distribution of sock sizes of volleyball players is different from the distribution of sock sizes that are currently being manufactured. If Ann's employer,
Foothill Hosiery, is going to market "Easy Bounce" socks to volleyball players, they are going to have to send out packages of samples that contain a different mix of sizes than they are
currently making. If "Easy Bounce" are successfully marketed to volleyball players, the mix of sizes manufactured will have to be altered.
, which is well into the "unusual" range which starts at 9.24 according to her decision rule. Ann has found that her sample data
supports the hypothesis that the distribution of sock sizes of volleyball players is different from the distribution of sock sizes that are currently being manufactured. If Ann's employer,
Foothill Hosiery, is going to market "Easy Bounce" socks to volleyball players, they are going to have to send out packages of samples that contain a different mix of sizes than they are
currently making. If "Easy Bounce" are successfully marketed to volleyball players, the mix of sizes manufactured will have to be altered.
Now, review what Ann has done to test to see if the data in her sample supports the hypothesis that the world is "unsurprising" and that volleyball players have the same distribution of sock
sizes as Foothill Hosiery is currently producing for other athletes. The essence of Ann's test was to see if her sample 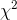 could easily have come from the sampling distribution of
could easily have come from the sampling distribution of 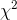 's generated by taking samples from the population of socks currently being produced. Since her sample
's generated by taking samples from the population of socks currently being produced. Since her sample 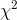 would be way out in the tail of that sampling distribution, she judged that her sample
data supported the other hypothesis, that there is a difference between volleyball players and the athletes who are currently buying "Easy Bounce" socks.
would be way out in the tail of that sampling distribution, she judged that her sample
data supported the other hypothesis, that there is a difference between volleyball players and the athletes who are currently buying "Easy Bounce" socks.
Formally, Ann first wrote null and alternative hypotheses, describing the population her sample comes from in two different cases. The first case is the null hypothesis; this occurs if
volleyball players wear socks of the same sizes in the same proportions as Foothill is currently producing. The second case is the alternative hypothesis; this occurs if volleyball players wear
different sizes. After she wrote her hypotheses, she found that there was a sampling distribution that statisticians knew about that would help her choose between them. This is the 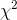 distribution. Looking at the formula for computing
distribution. Looking at the formula for computing 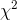 and consulting the tables, Ann decided that a sample
and consulting the tables, Ann decided that a sample 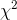 value greater than 9.24 would be unusual if her null hypothesis was true. Finally, she
computed her sample statistic, and found that her
value greater than 9.24 would be unusual if her null hypothesis was true. Finally, she
computed her sample statistic, and found that her 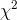 , at 26.46,
was well above her cut-off value. Ann had found that the data in her sample supported the alternative, Ha : , that the distribution of volleyball players' sock
sizes is different from the distribution that Foothill is currently manufacturing. Acting on this finding, Ann will send a different mix of sizes in the sample packages she sends volleyball
coaches.
, at 26.46,
was well above her cut-off value. Ann had found that the data in her sample supported the alternative, Ha : , that the distribution of volleyball players' sock
sizes is different from the distribution that Foothill is currently manufacturing. Acting on this finding, Ann will send a different mix of sizes in the sample packages she sends volleyball
coaches.
- 1720 reads





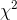 =
=

