Normal things

Available under Creative Commons-ShareAlike 4.0 International License.

Normal distributions are bell-shaped and symmetric. The mean, median, and mode are equal. Most of the members of a normally distributed population have values close to the mean—in a normal population 96 per cent of the members (much better than Chebyshev's 75 per cent), are within 2 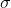$\sigma$ of the mean.

Statisticians have found that many things are normally distributed. In nature, the weights, lengths, and thicknesses of all sorts of plants and animals are normally distributed. In manufacturing, the diameter, weight, strength, and many other characteristics of man-or machine-made items are normally distributed. In human performance, scores on objective tests, the outcomes of many athletic exercises, and college student grade point averages are normally distributed. The normal distribution really is a normal occurrence.

If you are a skeptic, you are wondering how can GPAs and the exact diameter of holes drilled by some machine have the same distribution—they are not even measured with the same units. In order to see that so many things have the same normal shape, all must be measured in the same units (or have the units eliminated)—they must all be "standardized." Statisticians standardize many measures by using the STANDARD deviation. All normal distributions have the same shape because they all have the same relative frequency distribution when the values for their members are measured in standard deviations above or below the mean.

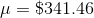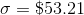Using the United States customary system of measurement, if the weight of pet cats is normally distributed with a mean of 10.8 pounds and a standard deviation of 2.3 pounds and the daily sales at The First Brew Expresso Cafe are normally distributed with $\mu=\$ 341.46$ and $\sigma=\$53.21$ , then the same proportion of pet cats weigh between 8.5 pounds ( 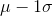$\mu-1\sigma$ ) and 10.8 pounds ( 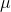$\mu$ ) as the proportion of daily First Brew sales which lie between 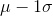$\mu-1\sigma$ ($288.25) and 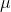$\mu$ ($341.46). Any normally distributed population will have the same proportion of its members between the mean and one standard deviation below the mean. Converting the values of the members of a normal population so that each is now expressed in terms of standard deviations from the mean makes the populations all the same. This process is known as "standardization" and it makes all normal populations have the same location and shape.

This standardization process is accomplished by computing a "z-score" for every member of the normal population. The z-score is found by:
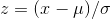
$z=(x-\mu)/\sigma$

This converts the original value, in its original units, into a standardized value in units of "standard deviations from the mean." Look at the formula. The numerator is simply the difference between the value of this member of the population, x, and the mean of the population 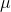$\mu$ . It can be measured in centimeters, or points, or whatever. 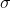The denominator is the standard deviation of the population, $\sigma$ , and it is also measured in centimeters, or points, or whatever. If the numerator is 15cm and the standard deviation is 10cm, then the z will be 1.5. This particular member of the population, one with a diameter 15cm greater than the mean diameter of the population, has a z-value of 1.5 because its value is 1.5 standard deviations greater than the mean. 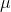Because the mean of the x's is $\mu$ , the mean of the z-scores is zero.

We could convert the value of every member of any normal population into a z-score. If we did that for any normal population and arranged those z-scores into a relative frequency distribution, they would all be the same. Each and every one of those standardized normal distributions would have a mean of zero and the same shape. There are many tables which show what proportion of any normal population will have a z-score less than a certain value. Because the standard normal distribution is symmetric with a mean of zero, the same proportion of the population that is less than some positive z is also greater than the same negative z. Some values from a "standard normal" table appear below:

Proportion below	.75	.90	.95	.975	.99	.995
z-score	0.674	1.282	1.645	1.960	2.326	2.576

John McGrath has asked Kevin Schmidt "How much does a pair of size 11 mens dress socks usually weigh?" Kevin asks the people in quality control what they know about the weight of these socks and is told that the mean weight is 4.25 ounces with a standard deviation of .021 ounces. Kevin decides that Mr. McGrath probably wants more than the mean weight, and decides to give his boss the range of weights within which 95% of size 11 men's dress socks falls. Kevin sees that leaving 2.5% (.025) in the left tail and 2.5% (.025) in the right tail will leave 95% (.95) in the middle. He assumes that sock weights are normally distributed, a reasonable assumption for a machine-made product, and consulting a standard normal table, sees that .975 of the members of any normal population have a z-score less than 1.96 and that .975 have a z-score greater than -1.96, so .95 have a z-score between ±1.96.

Now that he knows that 95% of the socks will have a weight with a z-score between ±1.96, Kevin can translate those z's into ounces. By solving the equation for both +1.96 and -1.96, he will find the boundaries of the interval within which 95% of the weights of the socks fall:
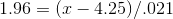
1.96=(x-4.25)/.021
solving for x, Kevin finds that the upper limit is 4.29 ounces. He then solves for z=-1.96:
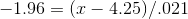
-1.96=(x-4.25)/.021
and finds that the lower limit is 4.21 ounces. He can now go to John McGrath and tell him: "95% of size 11 mens' dress socks weigh between 4.21 and 4.29 ounces."

897 reads

You are here

Normal things